Cho tam giác ABC có ba góc nhọn, nội tiếp đường tròn (O), các đường cao AM, BN, CP của tam giác ABC đồng quy tại H(M thuộc BC, N thuộc AC, P thuộc AB).
a/ Chứng minh tứ giác MHNC nội tiếp đường tròn.
b/ Kéo dài AH cắt (O) tại điểm thứ hai là D. Chứng minh: DBC=NBC
c/ Tiếp tuyến tại C của đường tròn ngoại tiếp tứ giác MHNC cắt đường thẳng AD tại K. Chứng minh: KM.KH + HC2 = KH2 .
.


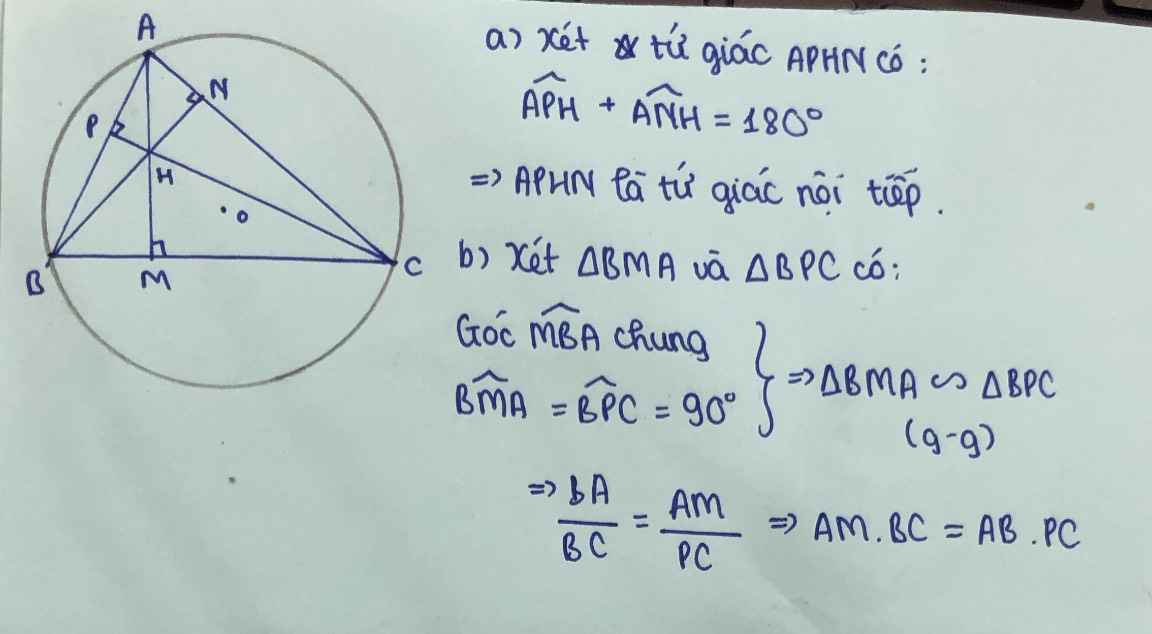

a: Xét tứ giác MHNC có \(\widehat{HMC}+\widehat{HNC}=90^0+90^0=180^0\)
nên MHNC là tứ giác nội tiếp
b: Xét (O) có
\(\widehat{DBC}\) là góc nội tiếp chắn cung DC
\(\widehat{DAC}\) là góc nội tiếp chắn cung DC
Do đó: \(\widehat{DBC}=\widehat{DAC}\)
mà \(\widehat{DAC}=\widehat{NBC}\left(=90^0-\widehat{ACB}\right)\)
nên \(\widehat{DBC}=\widehat{NBC}\)