Cho hình bình hành ABCD.Lấy điểm E đối xứng với điểm D qua A,lấy F đối xứng với điểm D qua C.
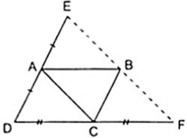
a)CM:AEBC là hình bình hành.
b)CM:ABFC là hình bình hành.Từ đó suy ra góc BAC=góc EFD.
c)CM:Điểm E và điểm F đối xứng với nhau qua điểm B.
d)Hình bình hành ABCD có thêm điều kiện gì thì điểm E đối xứng với điểm F qua đường thẳng BD.Vẽ hình minh họa

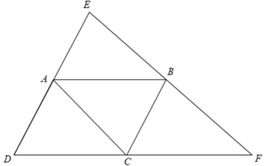
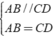
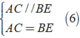
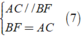
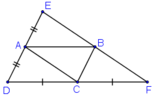
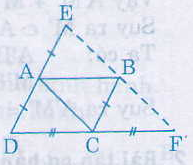
a) Do E đối xứng với D qua A nên AD = AE.
Do ABCD là hình bình hành nên AD = BC; AD //BC.
Xét tứ giác AEBC có AE//BC; AE = BC nên nó là hình bình hành (dấu hiệu nhận biết)
b)
Do F đối xứng với D qua C nên DC = CF.
Do ABCD là hình bình hành nên AB = DC; AB // DC.
Xét tứ giác ABFC có AB//CF; AB = CF nên nó là hình bình hành (dấu hiệu nhận biết)
Do ABFC là hình bình hành nên AC // BF.
Do AEBC là hình bình hành nên AC // BE.
Theo tiên đề Oclit suy ra E, B, F thẳng hàng.
Do ABFC là hình bình hành nên \(\widehat{BAC}=\widehat{BFD}\) (Hai góc đối)
Hay \(\widehat{BAC}=\widehat{EFD}\)
c) Ta đã có E, B, F thẳng hàng.
Lại có EB = AC; BF = AC nên EB = BF.
Vậy E và F đối xứng nhau qua B.
d) Để E và F đối xứng nhau qua đường thẳng BD thì \(BD\perp EF\)
Lại có EF // AC nên \(BD\perp AC\)
Hình bình hành ABCD có hai đường chéo vuông góc thì nó trở thành hình thoi.
Vậy hình bình hành ABCD trở thành hình thoi thì E và F đối xứng nhau qua BD.