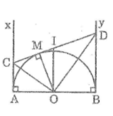
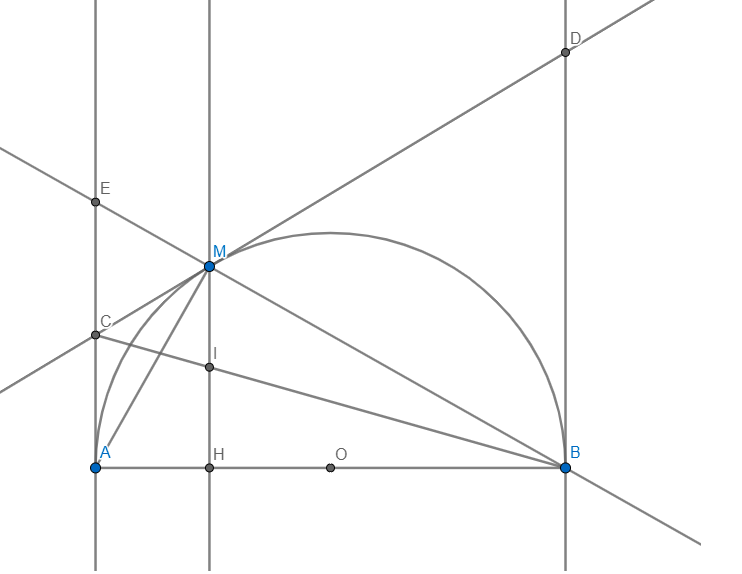
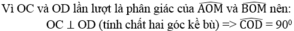Cho nửa đường tròn tâm O, AB là đường kính, kẻ các tuyến Ax và By ( ở cùng phía với nửa đường tròn ) E là một điểm thuộc nửa đường tròn, tiếp tuyến tại E cắt Ax, By tại C và D
a) Chứng minh rằng CD = AC + BD
b)Chứng minh rằng tam giác COD vuông
c) Gọi H là giao điểm của OC và AE, I là giao điểm của OD và BE, chứng minh rằng tứ giác HEIO là hình chữ nhật
d) Xác định vị trí của điểm E để tứ giác HEIO là hình vuông