Cho nửa đường tròn đường kính AB. Trên nửa đường tròn lấy C (C khác A, B). Gọi H là hình chiếu của C trên AB. Trên cung CB lấy D (D khác C, B). Hai đường thẳng AD và CH cắt tại E Chứng minha) tứ giác BDEH nội tiếp.b )Chứng minh AC^2 = AE.ADc ) gọi (O) là đường tròn qua D và tiếp xúc AB tại B ,(O') cắt CB tại F.Chứng minh...
Đọc tiếp
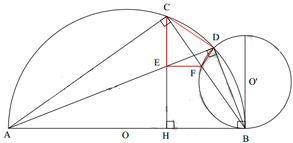
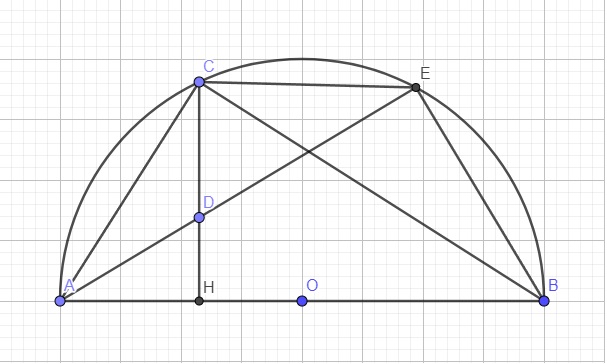
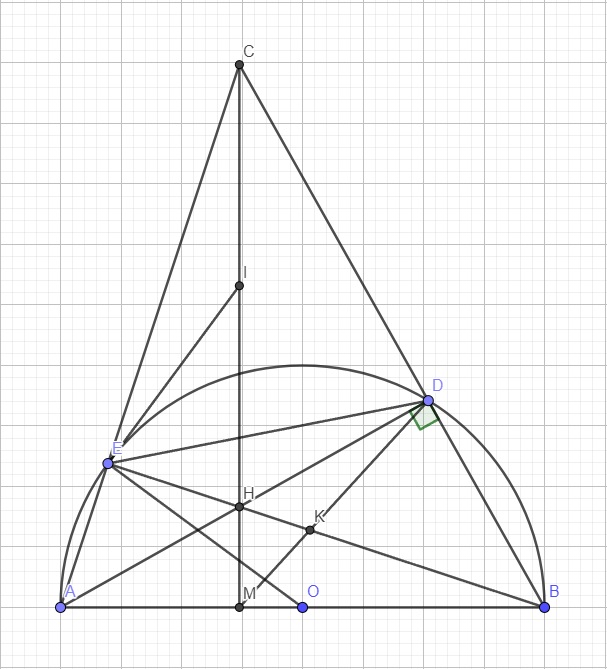
Cho nửa đường tròn đường kính AB. Trên nửa đường tròn lấy C (C khác A, B). Gọi H là hình chiếu của C trên AB. Trên cung CB lấy D (D khác C, B). Hai đường thẳng AD và CH cắt tại E Chứng minh
a) tứ giác BDEH nội tiếp.
b )Chứng minh AC^2 = AE.AD
c ) gọi (O) là đường tròn qua D và tiếp xúc AB tại B ,(O') cắt CB tại F.Chứng minh EF//AB
a) ta có góc ADB = 90 độ (góc nội tiếp chắn nửa đường tròn)
tứ giác BDEH có: góc EHB+ góc EDB = 90+90=180 độ
=> tứ giác BDEH nội tiếp
b) tứ giác ACDB nội tiếp ( do có 4 đỉnh nằm trên đường tròn)
=> góc ACD+góc DBA =180 độ
ta lại có góc HED+gócDBA=180 độ ( tứ giác DBHE nội tiếp)
=>góc ACD= gócHED
mà góc HED=gócAEC (đối đỉnh)
=> góc ACD=góc AEC
xét hai tam giác ACE và ADC có góc CAD chung ; góc ACD=gócAEC
=> △ACE đồng dạng △ADC(góc - góc)
=> \(\dfrac{AC}{AD}=\dfrac{AE}{AC}\)=>AC2=AD*AE