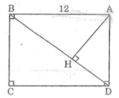
Cho hình chữ nhật ABCD có AB = a, BC = b. Kẻ CK vuông góc với BD tại K. Tính diện tích tam giác AKD theo a và b.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
KA
0
12 tháng 6 2020
Hình vẽ bị lỗi. Bạn thông cảm!
a) Xét \(\Delta\)KBA và \(\Delta\)CDB có:
^BKA = ^DCB = 90 độ
^KBA = ^CDB ( so le trong )
=> \(\Delta\)KBA ~ \(\Delta\)CDB (g-g)
b) Xét \(\Delta\)ADB có:
\(S\left(ADB\right)=\frac{1}{2}AD.AB=\frac{1}{2}AK.BD\)(1)
mà AB = 8cm ; AD = BC = 6cm ( ABCD là hình chữ nhật) ; BD = \(\sqrt{AD^2+AB^2}=\sqrt{6^2+8^2}=10\)(cm)
(1) => AD.AB = AK.BD => AK = 6.8 : 10 = 4,8 ( cm)
\(S\left(KBA\right)=\frac{1}{2}AK.KB\)
với KA = 4,8 cm và KB = \(\sqrt{AB^2-AK^2}=\sqrt{8^2-4,8^2}=6,4\)(cm)
=> \(S\left(KBA\right)=\frac{1}{2}AK.KB=\frac{1}{2}4,8.6,4=15,36\)(cm^2)
c) Áp dụng tính chất phân giác ta có:
\(\frac{BA}{BD}=\frac{FA}{FD};\frac{BK}{BA}=\frac{EK}{EA}\)(1)
Xét \(\Delta\)BAK và \(\Delta\)BDA có: ^BKA = ^BAD = 90 độ và ^B chung
=> \(\Delta\)BAK ~ \(\Delta\)BDA ( g-g)
-> \(\frac{BA}{BD}=\frac{BK}{BA}\)(2)
Từ (1); (2) => \(\frac{FA}{FD}=\frac{EK}{EA}\)=> EA.FA= EK.FD
CM
2 tháng 1 2019
Vì
△
AHB đồng dạng
△
BCD với tỉ số đồng dạng: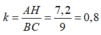 
Ta có: 
=
k
2
=
0
,
8
2
= 0,64 ⇒
S
A
H
B
=
0
,
64
.
S
B
C
D
S B C D = 1/2 BC.CD = 1/2 .12.9 = 54( c m 2 )
Vậy S A H B = 0 , 64 . S B C D = 0,64.54 = 34,56 ( c m 2 ).
4 tháng 7 2023
a: Xét ΔBCE vuông tại C và ΔDBE vuông tại B có
góc E chung
=>ΔBCE đồng dạng với ΔDBE
b: Xét ΔCBD vuông tại C và ΔHCB vuông tại H có
góc CBD=góc HCB
=>ΔCBD đồng dạng với ΔHCB
=>CB/HC=BD/CB
=>BC^2=HC*BD
c: CE=6^2/8=4,5cm
CH//DB
=>ΔEHC đồng dạng với ΔEBD
=>S EHC/S EBD=(EC/ED)^2=(4,5/12,5)^2=81/625