Cho tam giác ABC , BC =40 tia phân giác AD dài 45 đường cao AH =36 Tính BD , BC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
28 tháng 10 2016
ABCEHD
+) Kẻ AE là phân giác ngoài của góc BAC
Mà AD là phân giác của góc BAC nên AD vuông góc với AE => tam giác EAD vuông tại A
+) Áp dụng ĐL Pi - ta go trong tam giác vuông AHD có: DH = √AD2−AH2=√452−362=27 cm
+) Áp dụng hệ thức lượng trong tam giác vuông EAD có: AD2 = DH. DE => DE = AD2 / DH = 452/ 27 = 75 cm
+)Áp dụng tính chất tia phân giác trong và ngoài tam giác có: BDDC =ABAC =EBEC
Đặt BD = x (0 < x < 40) => CD = 40 - x. Ta có:
x40−x =75−x75+(40−x) (do EB = DE - BD; EC = DE + DC)
=> x. (115 - x) = (40 - x).(75 - x)
<=> 115x - x2 = 3000 - 115x + x2 <=> x2 - 115x + 1500 = 0
=> x = 100 (Loại) hoặc x = 15 (thoả mãn)
Vậy BD = 15 cm hoặc BD = 40 - 15 = 25 cm (Nếu ta đổi vị trí B và C cho nhau)
MT
1
25 tháng 6 2021
ABCEHD
+) Kẻ AE là phân giác ngoài của góc BAC
Mà AD là phân giác của góc BAC nên AD vuông góc với AE => tam giác EAD vuông tại A
+) Áp dụng ĐL Pi - ta go trong tam giác vuông AHD có: DH = √AD2−AH2=√452−362=27 cm
+) Áp dụng hệ thức lượng trong tam giác vuông EAD có: AD2 = DH. DE => DE = AD2 / DH = 452/ 27 = 75 cm
+)Áp dụng tính chất tia phân giác trong và ngoài tam giác có: BDDC =ABAC =EBEC
Đặt BD = x (0 < x < 40) => CD = 40 - x. Ta có:
x40−x =75−x75+(40−x) (do EB = DE - BD; EC = DE + DC)
=> x. (115 - x) = (40 - x).(75 - x)
<=> 115x - x2 = 3000 - 115x + x2 <=> x2 - 115x + 1500 = 0
=> x = 100 (Loại) hoặc x = 15 (thoả mãn)
Vậy BD = 15 cm hoặc BD = 40 - 15 = 25 cm (Nếu ta đổi vị trí B và C cho nhau)
29 tháng 7 2023
BC=căn 3^2+4^2=5cm
AD là phân giác
=>BD/AB=CD/AC
=>BD/3=CD/4
=>BD/3=CD/4=5/7
=>BD=15/7cm; CD=20/7cm
12 tháng 3 2023
\(BC=\sqrt{3^2+4^2}=5\left(cm\right)\)
Xet ΔABC có AD là phân giác
nên BD/AB=CD/AC
=>BD/3=CD/4=(BD+CD)/(3+4)=5/7
=>BD=15/7cm; CD=20/7cm
10 tháng 5 2023
a: Xét ΔABC vuông tại A và ΔHAC vuông tại H có
góc C chung
=>ΔABC đồng dạng với ΔHAC
b: \(BC=\sqrt{3^2+4^2}=5\left(cm\right)\)
AH=3*4/5=2,4cm
c: góc AED=góc BEH=90 độ-góc EBH
góc ADE=90 độ-góc ABD
góc EBH=góc ABD
=>góc AED=góc ADE
=>AE=AD
PK
1 tháng 3 2023
Xét tam giác vuông ABC có:
BC^2=AB^2+AC^2
BC^2=6^2+8^2
BC=√6^2+8^2=10cm
Xét tam giác ABC có CD phân giác:
AD/BD=AC/BC(t/chất đường phân giác )
<=>AD+BD/BD=AC+BC/BC
<=>6/BD=18/10
<=>BD=10.6/18≈3,3cm
Ta có : AD+BD=AB
=>AD=AB-BD=6-3,3=2,7
NV
Nguyễn Việt Lâm
Giáo viên
28 tháng 7 2021
Trong tam giác vuông ABH:
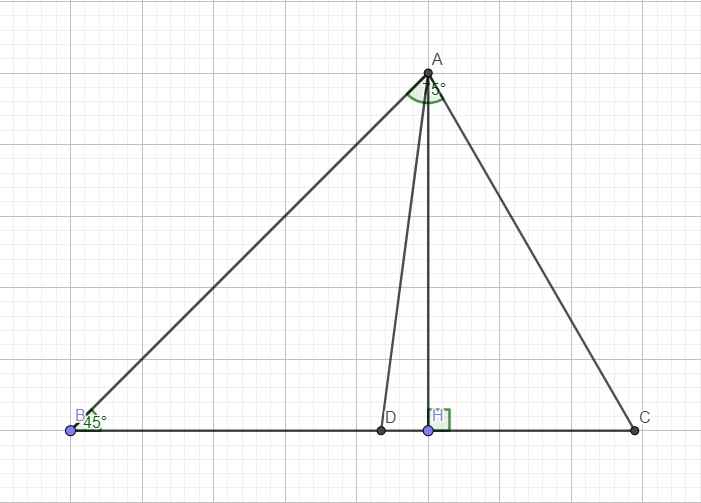
\(tanB=\dfrac{AH}{BH}\Rightarrow AH=BH.tanB=10.tan45^0=10\)
\(cosB=\dfrac{BH}{AB}\Rightarrow AB=\dfrac{BH}{cosB}=\dfrac{10}{cos45^0}=10\sqrt{2}\)
Do tam giác ABH vuông tại H \(\Rightarrow\widehat{BAH}=90^0-\widehat{B}=45^0\)
\(\Rightarrow\widehat{CAH}=\widehat{A}-\widehat{BAH}=75^0-45^0=30^0\)
Trong tam giác vuông ACH:
\(cos\widehat{CAH}=\dfrac{AH}{AC}\Rightarrow AC=\dfrac{AH}{cos\widehat{CAH}}=\dfrac{10}{cos30^0}=\dfrac{20\sqrt{3}}{3}\)
AD là phân giác góc A \(\Rightarrow\widehat{CAD}=\dfrac{1}{2}\widehat{A}=\dfrac{75^0}{2}=37^030'\)
\(\Rightarrow\widehat{DAH}=\widehat{CAD}-\widehat{CAH}=37^030'-30^0=7^030'\)
Trong tam giác vuông ADH:
\(cos\widehat{DAH}=\dfrac{AH}{AD}\Rightarrow AD=\dfrac{AH}{cos\widehat{DAH}}=\dfrac{10}{cos\left(7^030'\right)}\approx10,1\)
+ Kẻ AE là là phân giác của góc BAC
Mà AD là phân giác của góc BAC nên AD vuông góc với AE \(\Rightarrow\)tam giác EAD vuông góc tại A
+ Áp dụng định lí Pi-ta-go trong tam giác vuông AHD có: \(DH=\sqrt{AD^2-AH^2}=\sqrt{45^2-36^2}=27cm\)
+ Áp dụng hệ thức lượng giác trong tam giác vuông EAD có: \(AD^2=DH.DE\Rightarrow DE=\frac{AH^2}{DH}=\frac{45^2}{27}=75cm\)
+ Áp dụng tính chất phân giác trong và ngoài tam giác có: \(\frac{BD}{DC}=\frac{AB}{AC}=\frac{EB}{EC}\)
Đặt: \(BD=x0< x< 40\Rightarrow CD=40-x\), ta có:
\(\frac{x}{40-x}=\frac{75-x}{75+40-x}\)do \(EB=DE-BD;EC=DE+DC\)
\(\Rightarrow x.115-x=40-x.75-x\)
\(\Leftrightarrow115x-x^2=3000-115x+x^2\Leftrightarrow x^2-115x+1500=0\)
\(\Rightarrow x=100\)loại hoặc \(x=15\)thoả mãn
Vậy: \(BD=15cm\)hoặc \(BD=40-15=25cm\). Nếu ta đổi vị trí B và C cho nhau
P/s: Câu hỏi của thang Tran - Toán lớp 9 - Học toán với OnlineMath
thanks ban nha