cho tam giác abc vuông tại a có đường cao ah. a/ cm AC ^2 = CH.BC b/ Vẽ BD là tia pg góc ABC ( D thuộc AC) , BD cát AH tại I . cm tam giác ABI đồng dạng tam giác BDC và AID cân
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
10 tháng 5 2023
a: Xét ΔABC vuông tại A và ΔHAC vuông tại H có
góc C chung
=>ΔABC đồng dạng với ΔHAC
b: \(BC=\sqrt{3^2+4^2}=5\left(cm\right)\)
AH=3*4/5=2,4cm
c: góc AED=góc BEH=90 độ-góc EBH
góc ADE=90 độ-góc ABD
góc EBH=góc ABD
=>góc AED=góc ADE
=>AE=AD
LD
30 tháng 3 2022
a, Xét ΔABC và ΔHBA có :
\(\widehat{A}=\widehat{AHB}=90^0\)
\(\widehat{B}:chung\)
\(\Rightarrow\Delta ABC\sim\Delta HBA\left(g-g\right)\)
b, Xét ΔABC vuông tại A, theo định lý Pi-ta-go ta có :
\(BC=\sqrt{AB^2+AC^2}=\sqrt{6^2+8^2}=10\left(cm\right)\)
Ta có : \(\Delta ABC\sim\Delta HBA\left(cmt\right)\)
\(\Rightarrow\dfrac{AC}{AH}=\dfrac{BC}{AB}\)
hay \(\dfrac{8}{AH}=\dfrac{10}{6}\)
\(\Rightarrow AH=\dfrac{8.6}{10}=4,8\left(cm\right)\)
c, Xét ΔAHB và ΔCHA có :
\(\widehat{BHA}=\widehat{AHC}=90^0\)
\(\widehat{BAH}=\widehat{C}\left(phụ\cdot với\cdot\widehat{B}\right)\)
\(\Rightarrow\Delta AHB\sim\Delta CHA\left(g-g\right)\)
\(\Rightarrow\dfrac{AH}{HC}=\dfrac{BH}{AH}\)
\(\Rightarrow AH^2=HC.BH\)
d, Xét ΔABD và ΔHBI có :
\(\widehat{H}=\widehat{A}=90^0\)
\(\widehat{ABD}=\widehat{HBI}\left(phân\cdot giác\cdot BD\right)\)
\(\Rightarrow\Delta ABD\sim\Delta HBI\left(g-g\right)\)
\(\Rightarrow\dfrac{AB}{HB}=\dfrac{BD}{BI}\)
\(\Rightarrow AB.BI=BD.HB\left(đpcm\right)\)
19 tháng 8 2021
a: Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=100\)
hay BC=10cm
Xét ΔABC có BD là đường phân giác ứng với cạnh AC
nên \(\dfrac{AD}{AB}=\dfrac{CD}{BC}\)
hay \(\dfrac{AD}{6}=\dfrac{CD}{10}\)
mà AD+CD=8
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{AD}{6}=\dfrac{CD}{10}=\dfrac{AD+CD}{6+10}=\dfrac{8}{16}=\dfrac{1}{2}\)
Do đó: AD=3cm; CD=5cm
b: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
\(\widehat{ABC}\) chung
Do đó: ΔABC\(\sim\)ΔHBA
Suy ra: \(\dfrac{BA}{BH}=\dfrac{BC}{BA}\)
hay \(AB^2=BH\cdot BC\)
19 tháng 8 2021
c) Ta có: \(\widehat{ABD}=\widehat{DBC}\)( BD là phân giác )\(\Rightarrow90^0-\widehat{ABD}=90^0-\widehat{DBC}\Rightarrow\widehat{BIH}=\widehat{ADI}\Rightarrow\widehat{AID}=\widehat{ADI}\Rightarrow\Delta ADI\) cân tại A\(\Rightarrow AI=AD\Rightarrow\dfrac{AB}{AI}=\dfrac{AB}{AD}\)
Xét Δ ABI và Δ CBD có:
\(\widehat{BAI}=\widehat{BCD}\left(\Delta ABC\sim\Delta HBA\right)\)
\(\dfrac{AB}{AI}=\dfrac{BC}{CD}\left(=\dfrac{AB}{AD}\right)\)
\(\Rightarrow\Delta ABI\sim\Delta CBD\left(c.g.c\right)\)
d) Xét ΔABH có:
BI là tia phân giác của \(\widehat{ABH}\)
\(\Rightarrow\dfrac{IH}{IA}=\dfrac{BH}{AB}\left(1\right)\)( tính chất tia phân giác)
Xét ΔABC có:
BD là tia phân giác của \(\widehat{ABC}\)
\(\Rightarrow\dfrac{AD}{DC}=\dfrac{AB}{BC}\left(2\right)\)( tính chất tia phân giác)
Ta có: \(\dfrac{BH}{AB}=\dfrac{AB}{BC}\left(\Delta ABC\sim\Delta HBA\right)\left(3\right)\)
Từ \(\left(1\right),\left(2\right),\left(3\right)\Rightarrow\dfrac{IH}{IA}=\dfrac{AD}{DC}\left(đpcm\right)\)
7 tháng 4 2022
a: Xét ΔABD vuông tại A và ΔHBI vuông tại H có
\(\widehat{ABD}=\widehat{HBI}\)
Do đó: ΔABD\(\sim\)ΔHBI
b: Xét ΔABC vuông tại A có AH là đường cao
nên \(AH^2=HB\cdot HC\)
26 tháng 4
A) Ta cần chứng minh tam giác \(ABD\) đồng dạng tam giác \(HBI\). Để làm điều này, ta cần chứng minh rằng các góc của chúng là bằng nhau.
- Góc \(ABD\) và \(HBI\) là góc vuông, vì \(AB\) và \(HB\) là đường cao của tam giác \(ABC\).
- Góc \(ADB\) và \(HIB\) là góc phân giác của tam giác \(ABC\), do đó chúng bằng nhau.
Vậy, ta có thể kết luận tam giác \(ABD\) đồng dạng tam giác \(HBI\).
B) Để chứng minh \(AH^2 = HB \cdot HC\), ta sử dụng định lý đường cao và tính chất của đường cao trong tam giác vuông:
- \(AH\) là đường cao của tam giác \(ABC\), nên \(AH^2 = BH \cdot HC\).
Vậy, \(AH^2 = HB \cdot HC\).
C) Để chứng minh tam giác \(IAD\) cân và \(DA^2 = DC \cdot IH\), ta sử dụng tính chất của giao điểm của đường phân giác và đường cao:
- Góc \(IAD\) và \(IDA\) là góc phân giác của tam giác \(ABC\), do đó chúng bằng nhau.
- \(IH\) là đường cao của tam giác \(ABC\) nên \(DA^2 = DC \cdot IH\).
Vậy, ta chứng minh được tam giác \(IAD\) cân và \(DA^2 = DC \cdot IH\).
D) Để chứng minh \(K, P, Q\) thẳng hàng, ta có thể sử dụng tính chất của điểm trung điểm và đường phân giác:
- \(Q\) là trung điểm của \(BC\), nên \(Q\) nằm trên đường thẳng \(KP\).
- \(K\) là giao điểm của \(AH\) và \(BD\), và \(P\) là giao điểm của \(AH\) và \(CI\), nên \(K, P, Q\) thẳng hàng theo Định lý Menelaus trên tam giác \(ACI\) và đường thẳng \(KQ\).
Vậy, ta đã chứng minh được \(K, P, Q\) thẳng hàng.
25 tháng 4 2023
a: Xét ΔBAH vuông tại H và ΔBCA vuông tại A có
góc B chung
=>ΔBAH đồng dạng vói ΔBCA
b: Xét ΔBAD và ΔBHI có
góc BAD=góc BHI
góc ABD=góc HBI
=>ΔBAD đồng dạng vói ΔBHI
=>BA/BH=BD/BI
=>BA*BI=BH*BD
21 tháng 3 2023
a: \(CB=\sqrt{9^2+12^2}=15\left(cm\right)\)
ADlà phân giác
=>BD/AB=CD/AC
=>BD/3=CD/4=(BD+CD)/(3+4)=15/7
=>BD=45/7cm; CD=60/7cm
b: Xét ΔABH vuông tại H và ΔCDE vuông tại E có
góc HAB=góc ECD
=>ΔABH đồng dạng với ΔCDE
28 tháng 6 2023
a: Xét ΔABC vuông tại A và ΔHAC vuông tại H có
góc C chung
=>ΔABC đồng dạg với ΔHAC
b: BC=căn 3^2+4^2=5cm
AH=3*4/5=2,4cm
c: góc ADE=90 độ-góc ABD
góc AED=góc BEH=90 độ-góc DBC
mà góc ABD=góc DBC
nên góc ADE=góc AED
=>AD=AE
22 tháng 6 2023
a: Xét ΔABC vuông tại A và ΔHAC vuông tại H có
góc C chung
=>ΔABC đồng dạng với ΔHAC
b: BC=căn 3^2+4^2=5cm
AH=3*4/5=2,4cm
c: góc AED=góc BEH=90 độ-góc DBC
góc ADE=90 độ-góc ABD
mà góc DBC=góc ABD
nên góc AED=góc ADE
=>AD=AE
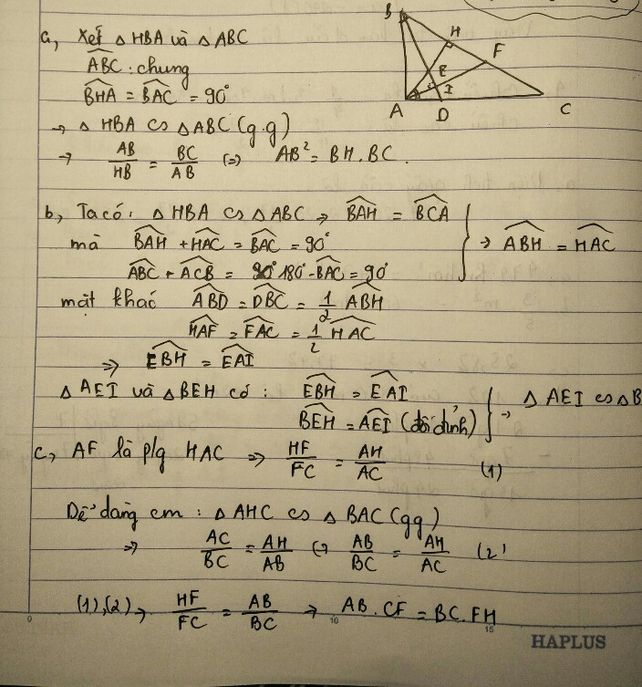
a: Xét ΔCHA vuông tại H và ΔCAB vuông tại A có
\(\widehat{HCA}\) chung
Do đó: ΔCHA~ΔCAB
=>\(\dfrac{CH}{CA}=\dfrac{CA}{CB}\)
=>\(CH\cdot CB=CA^2\)
b: Xét ΔBAI và ΔBCD có
\(\widehat{BAI}=\widehat{BCD}\left(=90^0-\widehat{HAC}\right)\)
\(\widehat{ABI}=\widehat{CBD}\)
Do đó: ΔBAI~ΔBCD
Ta có: \(\widehat{ADI}+\widehat{ABD}=90^0\)(ΔABD vuông tại A)
\(\widehat{HIB}+\widehat{HBI}=90^0\)(ΔHBI vuông tại H)
mà \(\widehat{ABD}=\widehat{HBI}\)
nên \(\widehat{ADI}=\widehat{HIB}\)
=>\(\widehat{ADI}=\widehat{AID}\)
=>ΔAID cân tại A