Câu 5: Cho tam giác ABC có BAC = 50
. Hai đường cao AAᇱ
và BB′ cắt nhau tại H. Trong các
khẳng định sau, khẳng định nào đúng?
A. Điểm H là trực tâm tam giác HBC B. Điểm H là trực tâm ∆HAC
C. HBC = HCA = 25
D. HBC + HCB = 50
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
H
1
Những câu hỏi liên quan
CM
18 tháng 2 2018
* Do O là tâm đường tròn ngoại tiếp tam giác ABC nên O là giao điểm của 3đường trung trực của tam giác ABC.
Lại có: M là trung điểm của BC nên O M ⊥ B C (OM là 1 đường trung trực của tam giác) (1)
* Lại có H là trực tâm của tam giác ABC nên: A H ⊥ B C (2)
Từ (1) và (2) suy ra: OM // AH.
* Nếu tam giác ABC nhọn thì O nằm trong tam giác ABC nên A H → , O M → cùng hướng
* Nếu tam giác ABC tù thì O nằm ngoài tam giác ABC nên A H → , O M → ngược hướng.
Đáp án A
21 tháng 9 2023
Tham khảo:
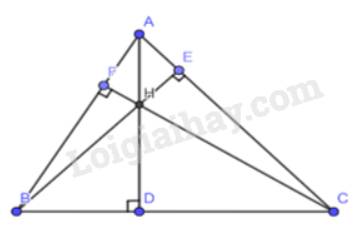
+) Xét tam giác HBC ta có :
HD vuông góc với BC \( \Rightarrow \) HD là đường cao tam giác HBC
BF vuông góc với HC tại F ( kéo dài HC ) \( \Rightarrow \)BF là đường cao của tam giác HBC
CE vuông góc với HB tại E ( kéo dài HB ) \( \Rightarrow \)CE là đường cao của tam giác HBC
Ta kéo dài HD, BF, CE sẽ cắt nhau tại A
\( \Rightarrow \) A là trực tâm tam giác HBC
+) Xét tam giác HAB ta có :
HF vuông góc với AB \( \Rightarrow \) HF là đường cao tam giác HAB
BH vuông góc với AE tại E ( kéo dài HB ) \( \Rightarrow \)AE là đường cao của tam giác HAB
BD vuông góc với AH tại D ( kéo dài AH ) \( \Rightarrow \)BD là đường cao của tam giác HAB
Ta kéo dài HF, BD, AE sẽ cắt nhau tại C
\( \Rightarrow \) C là trực tâm tam giác HAB
+) Xét tam giác HAC ta có :
HE vuông góc với AC \( \Rightarrow \) HE là đường cao tam giác HAC
AF vuông góc với HC tại F ( kéo dài HC ) \( \Rightarrow \)AF là đường cao của tam giác HAC
CD vuông góc với AH tại D ( kéo dài AH ) \( \Rightarrow \)CD là đường cao của tam giác HAC
Ta kéo dài CD, HE, AF sẽ cắt nhau tại B
\( \Rightarrow \) B là trực tâm tam giác HAC.
23 tháng 8 2021
a: Vì góc A nhọn nên chắc chắn tam giác ABC không thể vuông cân
=> Loại
b: Gọi giao điểm của BH và AC là K
=> BK\(\perp\)AC tại K
Ta có: ΔABK vuông tại K
nên \(\widehat{ABK}+\widehat{BAK}=90^0\)
hay \(\widehat{BAC}=60^0\)
Xét ΔABC cân tại A có \(\widehat{BAC}=60^0\)
nên ΔABC đều
CM
4 tháng 10 2017
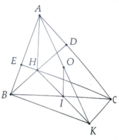
a, BHCK có I là trung điểm hai đường chéo
b, Ta có ∆ABK, ∆ACK vuông tại B và C nên A,B,K,C nằm trên đường tròn đường kính AK
c, Ta có OI là đường trung bình của ∆AHK => OI//AH
d, Gọi AH cắt BC tại M. Ta có BE.BA = BM.BC và CA.CD = CM.BC => ĐPCM
Chọn D