Cho hình bình hành ABCD tâm O.Trên đường chéo AC lấy 2 điểm I,J sao cho AI=IJ=JC.
a, Chứng minh: A và I đối xứng với nhau qua O
b, Tứ giác DIBJ nhận O làm tâm đối xứng.
c, DI cắt AB ở E , BJ cắt CD ở F. Chứng minh: E và F đối xứng với nhau qua O
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

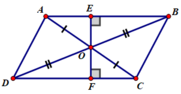
- Hình bình hành ABCD có O là giao điểm của hai đường chéo ⇒ O là trung điểm mỗi đường nên A và C đối xứng nhau qua tâm O
B và D đối xứng nhau qua tâm O
- Xét hai tam giác vuông AEO và CFO có:
OA = OC (do O là trung điểm AC)
∠(AOE) = ∠(COF)(hai góc đối đỉnh)
⇒ ΔAEO = ΔCFO (cạnh huyền – góc nhọn kề)
⇒ OE = OF (hai cạnh tương ứng)
Nên O là trung điểm EF
⇒ E và F đối xứng nhau qua tâm O

1: Xét ΔACE có
I là trung điểm của AE
O là trung điểm của AC
Do đó: IO là đường trung bình của ΔACE
Suy ra: IO//CE
hay OIEC là hình thang