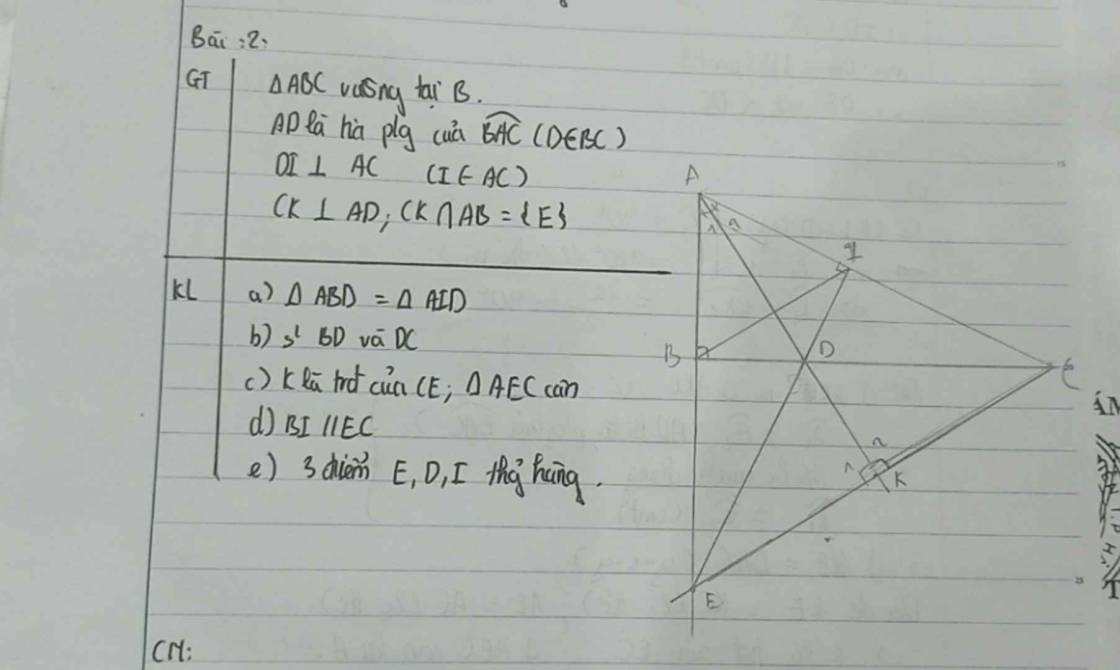
giup mik phan (e) vs a
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
SK
4
ND
3
RY
8 tháng 11 2018
Xét tam giác ABE :
\(\widehat{A}+\widehat{B}+\widehat{E}=180^0\\ \Rightarrow\widehat{B}=180^0-50^0-60^0=70^0\)
Lại có BO là phân giác của góc ABE
\(\Rightarrow\widehat{ABO}=\widehat{EBO}=\frac{70^0}{2}=65^0\)
Xét tam giác ABO :
\(\widehat{A}+\widehat{B}+\widehat{O}=180^0\\ \Rightarrow\widehat{AOB}=180^0-35^0-60^0=85^0\)
Xét tam giác EBO :
\(\widehat{E}+\widehat{B}+\widehat{O}=180^0\\ \Rightarrow\widehat{EOB}=180^0-35^0-50^0=95^0\)
Vậy \(\widehat{AOB}=85^0và\widehat{EOB}=95^0\)
RY
8 tháng 11 2018
Hình bạn tự vẽ nha!
Vì góc E = góc O nên tam giác AEO là tam giác cân.
\(\Rightarrow\widehat{A}=180^0-50^0-50^0\\ \Rightarrow\widehat{A}=80^0\)
Lại có AM là phân giác góc ngoài tại đỉnh A.
\(\Rightarrow\widehat{AMO}=\frac{180^0-80^0}{2}=50^0\left(=\widehat{E}\right)\)
Mà hai góc này nằm ở vị trí đồng vị nên EO // AM.
V
0
10 tháng 2 2019
Chiều cao là:
56 : [(4 + 3) x 2] = 4 m
Diện tích toàn phần là:
56 + 4 x 3 x 2 = 80 m2
Đáp số : ...
10 tháng 2 2019
Chiều cao hình hộp chữ nhật là :
\(56\div\left[(4+3)\cdot2\right]=4(m)\)
Diện tích toàn phần hình hộp chữ nhật là :
\(56+4\cdot3\cdot2=80(m^2)\)
Đáp số : ...
P/S : Hoq chắc :>
NV
Nguyễn Việt Dũng
CTVVIP
1 tháng 11 2023
Tham khảo
- Khí hậu châu Âu có sự phân hoá từ bắc xuống nam và từ tây sang đông tạo nên các đới và kiểu khí hậu khác nhau.
- Đới khí hậu cực và cận cực quanh năm giá lạnh, lượng mưa trung bình năm dưới 500 mm.
- Đới khí hậu ôn đới có sự phân hóa thành các kiểu khí hậu khác nhau.
+ Khí hậu ôn đới hải dương: ôn hòa, mùa đông tương đối ẩm mùa hạ mát, có mưa quanh năm, lượng mưa trung bình năm từ 800-1000 mm trở lên.
+ Khí hậu ôn đới lục địa: mùa đông lạnh và khô, mùa hạ nóng và ẩm. Lượng mưa nhỏ, trung bình năm chỉ trên dưới 500 mm, mưa chủ yếu vào mùa hạ.
- Đới khí hậu cận nhiệt ở châu Âu chỉ có một kiểu là cận nhiệt địa trung hải, mùa hạ nóng và khô, thời tiết ổn định; mùa đông ấm và mưa nhiều hơn. Lượng mưa trung bình năm khoảng 500 – 700 mm.
- Ngoài ra, khí hậu ở các vùng núi có sự phân hoá theo độ cao.
a: Xét ΔABD vuông tại B và ΔAID vuông tại I có
AD chung
\(\widehat{BAD}=\widehat{IAD}\)
Do đó: ΔABD=ΔAID
b: ta có: ΔABD=ΔAID
=>DB=DI
mà DI<DC(ΔDIC vuông tại I)
nên DB<DC
c: Xét ΔAEC có
AK là đường cao
AK là đường phân giác
Do đó: ΔAEC cân tại A
Ta có: ΔAEC cân tại A
mà AK là đường cao
nên K là trung điểm của EC
d: Xét ΔAEC có \(\dfrac{AB}{AE}=\dfrac{AI}{AC}\)
nên BI//EC
e: Xét ΔAEC có
AK,CB là các đường cao
AK cắt CB tại D
Do đó: D là trực tâm của ΔAEC
=>ED\(\perp\)AC
mà DI\(\perp\)AC
và ED,DI có điểm chung là D
nên E,D,I thẳng hàng