giúp e câu a với c với ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
8 tháng 5 2021
a, Ta có : \(\sin^2x+\cos^2x=1\)
\(\Rightarrow\sin x=\sqrt{1-\cos^2x}=\left|\dfrac{\sqrt{15}}{4}\right|\)
Mà \(0< x< \dfrac{\pi}{2}\)
\(\Rightarrow\sin x=\dfrac{\sqrt{15}}{4}\)
Ta lại có : \(\left\{{}\begin{matrix}\sin2x=2\sin x\cos x=\dfrac{\sqrt{15}}{8}\\\cos2x=2\cos^2x-1=-\dfrac{7}{8}\end{matrix}\right.\)
Vậy ...
c, Ta có : \(\tan2x=\dfrac{2\tan x}{1-\tan^2x}=\dfrac{4}{3}=\dfrac{\sin2x}{\cos2x}\)
- Ta có HPT : \(\left\{{}\begin{matrix}\sin^22x+\cos^22x=1\\3\sin2x-4\cos2x=0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\sin2x=\left|\dfrac{4}{5}\right|\\\cos2x=\left|\dfrac{3}{5}\right|\end{matrix}\right.\)
Lại có : \(\pi< x< \dfrac{3}{2}\pi\)
\(\Rightarrow\left\{{}\begin{matrix}\sin2x=\dfrac{4}{5}\\\cos2x=\dfrac{3}{5}\end{matrix}\right.\)
Vậy ...
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
11 tháng 2 2022
\(a,2KMnO_4\rightarrow\left(t^o\right)K_2MnO_2+MnO_2+O_2\\ b,n_{KMnO_4}=\dfrac{31,6}{158}=0,2\left(mol\right)\\ \Rightarrow n_{O_2}=\dfrac{0,2}{2}=0,1\left(mol\right)\\ \Rightarrow V_{O_2\left(đktc\right)}=0,1.22,4=2,24\left(l\right)\\ c,n_{Fe}=\dfrac{11,2}{56}=0,2\left(mol\right)\\ 3Fe+2O_2\rightarrow\left(t^o\right)Fe_3O_4\\ Vì:\dfrac{0,2}{3}< \dfrac{0,1}{2}\Rightarrow Fedư\\ \Rightarrow n_{Fe_3O_4}=n_{O_2}:2=0,1 :2=0,05\left(mol\right)\\ \Rightarrow m_{Fe_3O_4}=232.0,05=11,6\left(g\right)\)
H9
HT.Phong (9A5)
CTVHS
15 tháng 4 2023
a) \(N\left(x\right)=9-x^3+4x^3-7x+3x^2+x^2\)
\(N\left(x\right)=-\left(x^3-4x^3\right)+\left(3x^2+x^2\right)-7x+9\)
\(N\left(x\right)=3x^3+4x^2-7x+9\)
\(M\left(x\right)=4+6x^2+3x+5x^3-2x^3-2x^2\)
\(M\left(x\right)=\left(5x^3-2x^3\right)+\left(6x^2-2x^2\right)+3x+4\)
\(M\left(x\right)=3x^3+4x^2+3x+4\)
b) \(P\left(x\right)=N\left(x\right)-M\left(x\right)\)
\(P\left(x\right)=\left(3x^3+4x^2-7x+9\right)-\left(3x^2+4x^2+3x+4\right)\)
\(P\left(x\right)=3x^3+4x^2-7x+9-3x^3-4x^2-3x-4\)
\(P\left(x\right)=-10x+5\)
\(Q\left(x\right)=N\left(x\right)+M\left(x\right)\)
\(Q\left(x\right)=\left(3x^3+4x^2-7x+9\right)+\left(3x^3+4x^2+3x+4\right)\)
\(Q\left(x\right)=3x^3+4x^2-7x+9+3x^3+4x^2+3x+4\)
\(Q\left(x\right)=6x^3+8x^2-4x+13\)
c) Nghiệm của đa thức \(P\left(x\right)\)
\(P\left(x\right)=-10x+5=0\)
\(\Rightarrow-10x=-5\)
\(\Rightarrow10x=5\)
\(\Rightarrow x=\dfrac{5}{10}=\dfrac{1}{2}\)
Nghiệm của đa thức \(Q\left(x\right)\)
Vì: \(Q\left(x\right)=6x^3+8x^2+4x+13\ge0\)
\(\Rightarrow Q\left(x\right)\ge0\)
Vậy đa thức vô nghiệm
d) \(Q\left(x\right)\left(1-2x\right)\)
\(=\left(6x^3+8x^2-4x+13\right)\left(1-2x\right)\)
\(=6x^3+8x^2-4x+13-12x^4-16x^3+8x^2-26x\)
\(=-12x^4-10x^3+16x^2-30x+13\)
NH
mọi người giúp e câu c với ạ
0
16 tháng 6 2023
a: \(A=\dfrac{x\left(x+2\right)}{\left(x-2\right)^2}:\dfrac{x^2-4+x+6-x^2}{x\left(x-2\right)}\)
\(=\dfrac{x\left(x+2\right)}{x-2}\cdot\dfrac{x}{x+2}=\dfrac{x^2}{x-2}\)
c: A<0
=>x-2<0
=>x<2
d: B nguyên
=>x^2-4+4 chia hết cho x-2
=>x-2 thuộc {1;-1;2;-2;4;-4}
=>x thuộc {3;1;4;6}
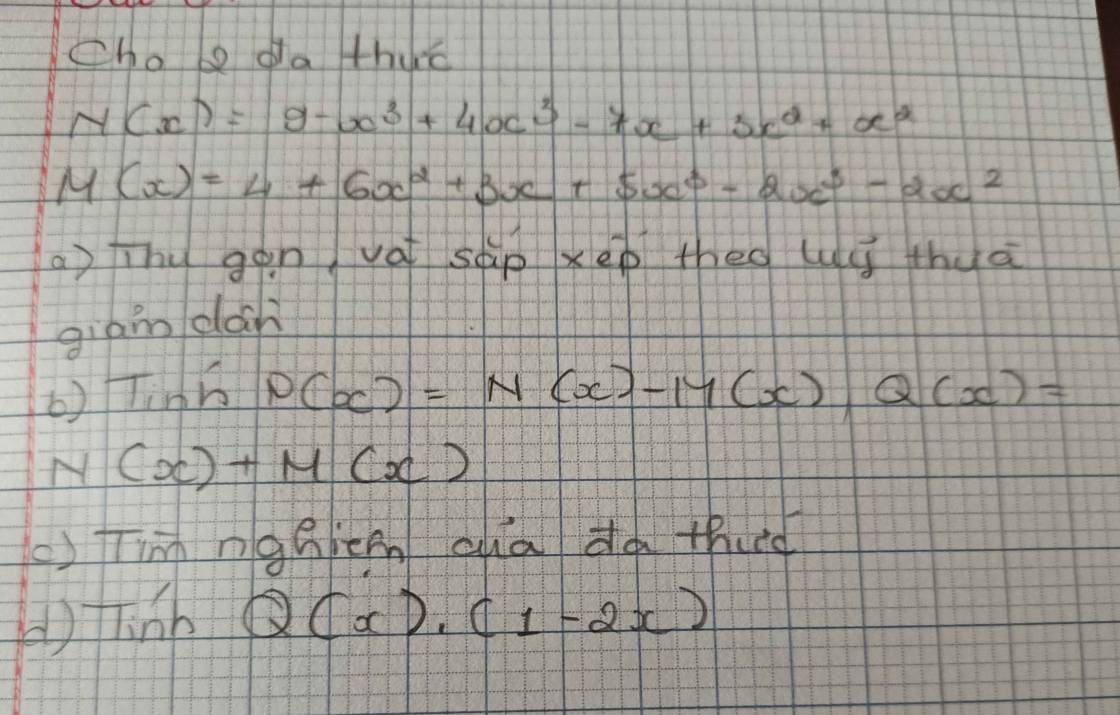
a) Hàm số trên có:
a = -3
b = -2
Đồ thị của hàm số cắt trục tung tại điểm (0; b) nên có tung độ là -2
b) Bảng giá trị:
Đồ thị:
d) Phương trình hoành độ giao điểm của (d) và (d'):
-3x - 2 = x + 3
-3x - x = 3 + 2
-4x = 5
x = -5/4
y = -5/4 + 3 = 7/4
Vậy tọa độ giao điểm của (d) và (d') là (-5/4; 7/4)