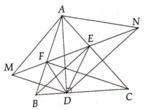
Bài 7: Cho ΔABC cân ở A có AD là trung tuyến, đường cao BE cắt ADở H. a) Chứng minh CH ⊥ AB. b) Vẽ điểm Isao cho A là trung điểm của CI, vẽ đường cao AK của ΔBAI. Tính KAD. c) AB cắt DK tại J. Chứng minh AB = DKvà J là trung điểm chung của AB và DK. d) Gọi O là trung điểm của AC. Trên tia đối của tia OB lấy điểm L sao cho OL = OB. Chứng minh K, A, L thẳng...
Đọc tiếp
Bài 7: Cho ΔABC cân ở A có AD là trung tuyến, đường cao BE cắt ADở H. a) Chứng minh CH ⊥ AB. b) Vẽ điểm Isao cho A là trung điểm của CI, vẽ đường cao AK của ΔBAI. Tính KAD. c) AB cắt DK tại J. Chứng minh AB = DKvà J là trung điểm chung của AB và DK. d) Gọi O là trung điểm của AC. Trên tia đối của tia OB lấy điểm L sao cho OL = OB. Chứng minh K, A, L thẳng hàng.
a:
ΔABC cân tại A
mà AD là đường trung tuyến
nên AD là phân giác của góc BAC và AD\(\perp\)BC
Xét ΔABC có
AD,BE là các đường cao
AD cắt BE tại H
Do đó: H là trực tâm của ΔABC
=>CH\(\perp\)AB
b: Xét ΔIBC có
BA là đường trung tuyến
\(BA=\dfrac{IC}{2}\)
Do đó; ΔIBC vuông tại B
Xét tứ giác BDAK có
\(\widehat{BDA}=\widehat{BKA}=\widehat{KBD}=90^0\)
=>BDAK là hình chữ nhật
=>\(\widehat{KAD}=90^0\)
c: BDAK là hình chữ nhật
=>AB=DK
BDAK là hình chữ nhật
=>BA cắt DK tại trung điểm của mỗi đường
=>J là trung điểm chung của BA và DK
d: Xét ΔOAL và ΔOCB có
OA=OC
\(\widehat{AOL}=\widehat{COB}\)(hai góc đối đỉnh)
OL=OB
Do đó: ΔOAL=ΔOCB
=>\(\widehat{OAL}=\widehat{OCB}\)
=>AL//CB
mà KA//BC
nên A,L,K thẳng hàng