Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a: Xét ΔAEB vuông tại E và ΔAFC vuông tại F co
góc A chung
=>ΔAEB đồng dạng với ΔAFC
b: ΔAEB đồng dạng với ΔAFC
=>AE/AF=AB/AC
=>AE*AC=AB*AF
a: Xét ΔABE vuông tại E và ΔACF vuông tại F có
góc BAE chung
=>ΔABE đồng dạng với ΔACF
=>AB/AC=AE/AF
=>AE/AB=AF/AC và AE*AC=AB*AF
b: Xét ΔAEF và ΔABC có
AE/AB=AF/AC
góc A chung
=>ΔAEF đồng dạng với ΔABC
=>góc AEF=góc ACB
c; góc AFH=góc AEH=90 độ
=>AFHE nội tiếp (I)
=>IF=IE
góc BFC=góc BEC=90 độ
=>BFEC nội tiếp (M)
=>MF=ME
=>MI là trung trực của EF
=>MI vuông góc EF
a, Xét tgABE và tgACF có:
góc AEB = góc CFA = 90o
góc BAC chung
Từ 2 điều trên => tgABE đồng dạng tgACF (g.g)
=> AB/AC = AE/AF (các cặp cạnh tương ứng)
=> AB.AF = AC.AE
hình tự kẻ ạ :3
a)
xét ΔABE và ΔACF có:
\(\left\{{}\begin{matrix}\widehat{A}\left(chung\right)\\\widehat{AFC}=\widehat{AEB}=90^0\left(CF\perp AB;BE\perp AC\right)\end{matrix}\right.\Rightarrow\Delta ABE\sim\Delta ACF\left(g.g\right)\)
\(\Rightarrow\dfrac{AC}{AB}=\dfrac{AF}{AE}\Leftrightarrow AC.AE=AB.AF\)
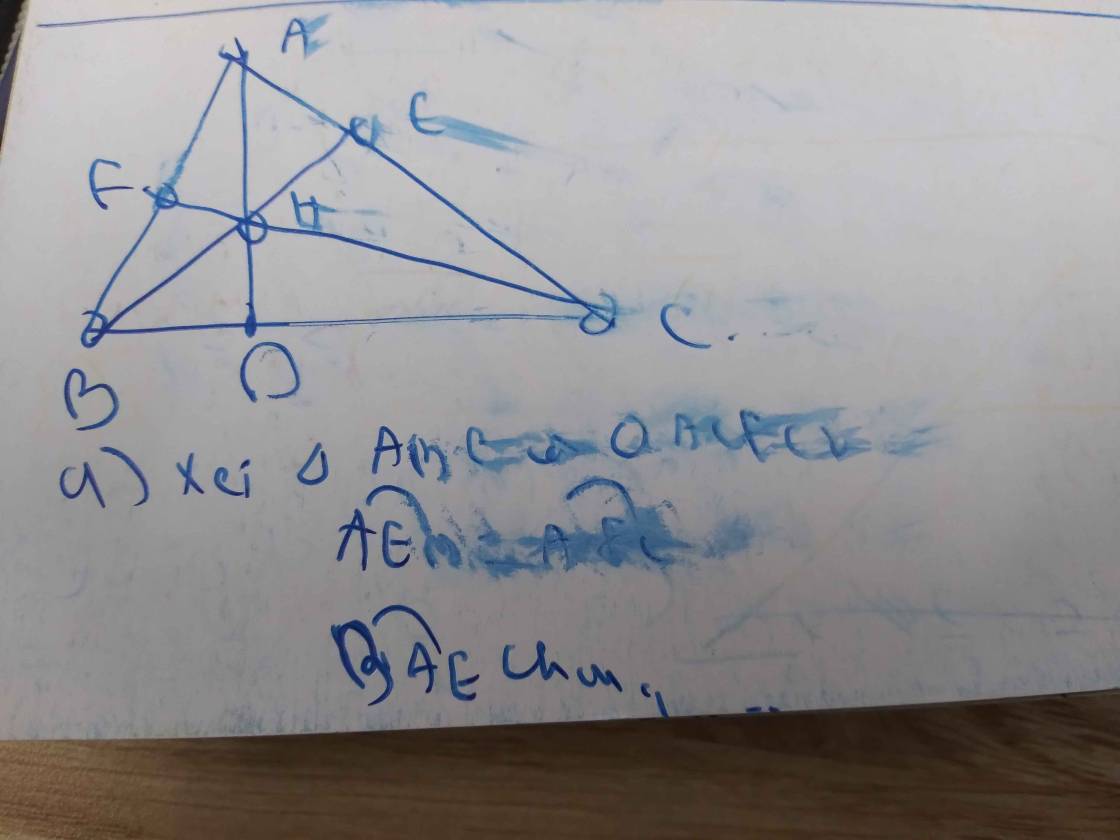
a: Xét ΔAEB vuông tại E và ΔAFC vuông tại F có
\(\widehat{BAE}\) chung
Do đó:ΔAEB~ΔAFC
=>\(\dfrac{AE}{AF}=\dfrac{AB}{AC}=\dfrac{EB}{FC}\)
b: Ta có: \(\dfrac{AE}{AF}=\dfrac{AB}{AC}\)
=>\(\dfrac{AE}{AB}=\dfrac{AF}{AC}\)
Xét ΔAEF và ΔABC có
\(\dfrac{AE}{AB}=\dfrac{AF}{AC}\)
\(\widehat{EAF}\) chung
Do đó: ΔAEF~ΔABC
=>\(\widehat{AEF}=\widehat{ABC}\)