ChChc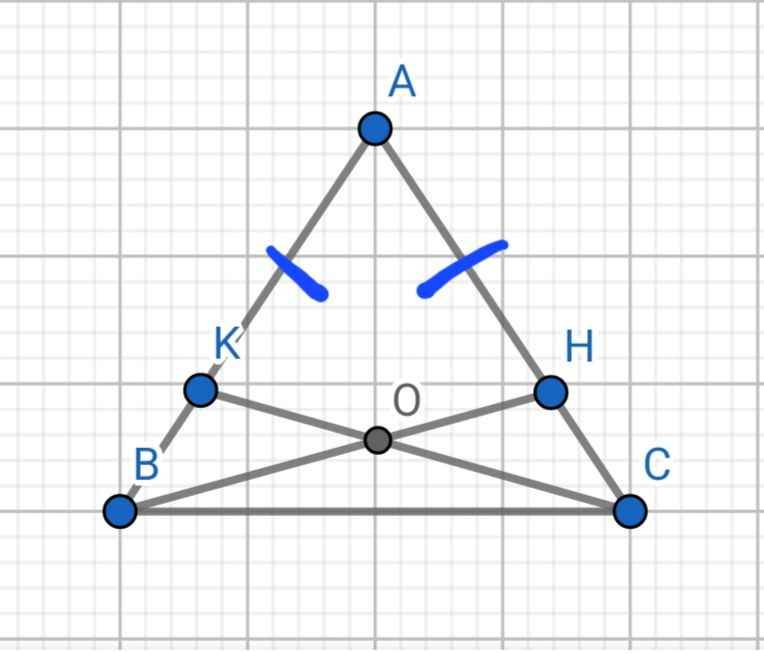 Chứng minh điểm O thuộc trung trực của đoạn thẳng BC
Chứng minh điểm O thuộc trung trực của đoạn thẳng BC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


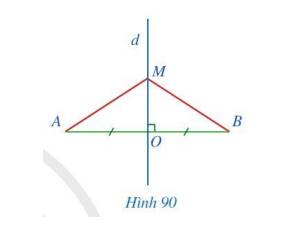
a) Ta có: d là đường trung trực của đoạn thẳng AB, điểm M thuộc d nên MO là đường trung trực của đoạn thẳng AB
\(\Rightarrow MO \bot AB \to \widehat {MOA} = \widehat {MOB} = 90^\circ \).
Xét tam giác MOA và tam giác MOB có:
OM chung;
\(\widehat {MOA} = \widehat {MOB} = 90^\circ \);
OA = OB (O là trung điểm của đoạn thẳng AB).
Vậy \(\Delta MOA = \Delta MOB\) (c.g.c)
b) \(\Delta MOA = \Delta MOB\) nên MA = MB ( 2 cạnh tương ứng)

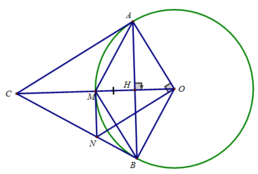
d) Ta có: CA ⊥ OA (CA là tiếp tuyến của (O)
và ON ⊥ OA (gt)
⇒ CA // ON ⇒ ∠(CON) = ∠(ACO) (sole trong)
Mà ∠(ACO) = ∠(BCO) (ΔOAC = ΔOBC)
⇒ ∠(CON) = ∠(BCO) ⇒ ΔNCO cân tại N
Xét tam giác CAO vuông tại A có ∠(AOC) = 60o( ΔAMO đều) nên:
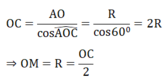
⇒ M là trung điểm của OC
ΔNCO cân tại N có NM là trung tuyến ⇒ NM cũng là đường cao
Hay NM là tiếp tuyến của (O)

Chứng minh tương tự như d suy ra CB // DE.
Do đó theo tiên đề Ơ-clit ta suy ra hai đường thẳng BC và CA trùng nhau hay A, B, C thẳng hàng.


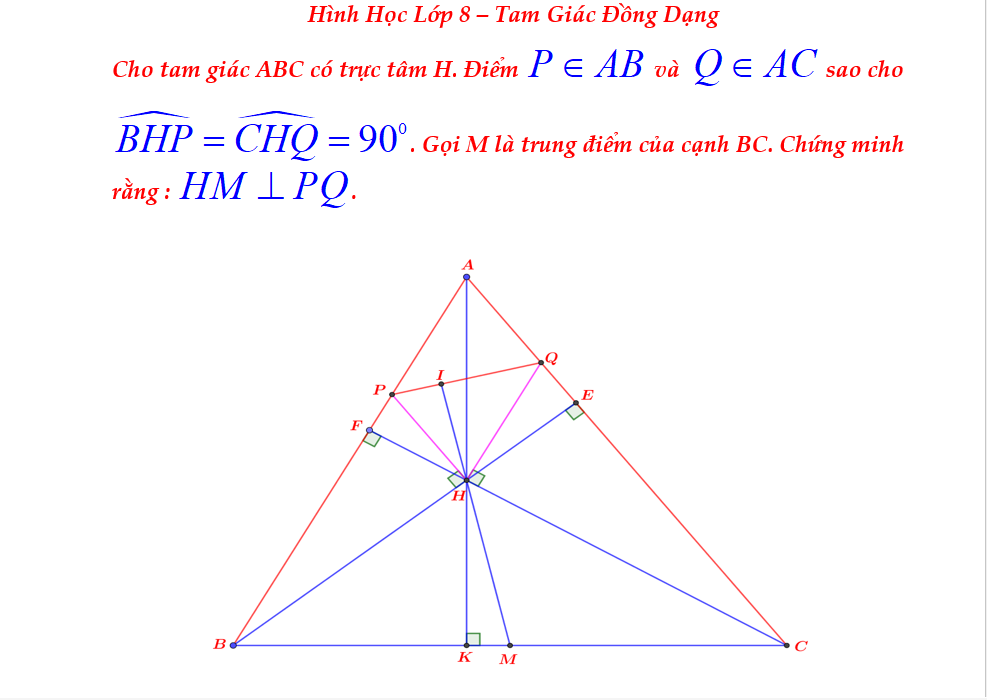
Qua C kẻ đường thẳng song với PQ, cắt AB tại N, cắt AH tại K
HP=HQ
=>KN=KC
=>KM là đường trung bình của ΔCBN
=>KM//NB
=>KM vuông góc CH
M là trực tâm của ΔCHK
=>HM vuông góc nC
=>HM vuông góc PQ

Ta có: AK+KB=AB
AH+HC=AC
mà AK=AH và AB=AC
nên KB=HC
Xét ΔKBC và ΔHCB có
KB=HC
\(\widehat{KBC}=\widehat{HCB}\)
CB chung
Do đó: ΔKBC=ΔHCB
=>\(\widehat{KCB}=\widehat{HBC}\)
=>\(\widehat{OBC}=\widehat{OCB}\)
=>ΔOBC cân tại O
=>OB=OC
=>O nằm trên đường trung trực của BC
Bạn nên ghi hẳn đề bài ra để mọi người hỗ trợ tốt hơn nhé.