 cho em hỏi câu 4 với ạ
cho em hỏi câu 4 với ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Do 2 đầu của R5 nối cùng một điện thế nên ta chập lại với nhau (mạch không còn R5).
Sơ đồ mạch điện lúc này: R1 nt (R2 // R3 // R4) nt R6
Ta có: \(\dfrac{1}{R_{234}}=\dfrac{1}{R_2}+\dfrac{1}{R_3}+\dfrac{1}{R_4}\)
\(\Rightarrow \dfrac{1}{R_{234}}=\dfrac{1}{9}+\dfrac{1}{18}+\dfrac{1}{6}\)
\(\Rightarrow R_{234}= 3 \Omega\)
Điện trở tương đương của mạch:
\(R_{tđ} = R_1+R_{234}+R_6=3+3+6=12\Omega\)

b) Để B nguyên thì \(3\sqrt{x}-2⋮2\sqrt{x}+1\)
\(\Leftrightarrow6\sqrt{x}-4⋮2\sqrt{x}+1\)
\(\Leftrightarrow-7⋮2\sqrt{x}+1\)
\(\Leftrightarrow2\sqrt{x}+1\in\left\{1;-1;7;-7\right\}\)
\(\Leftrightarrow2\sqrt{x}\in\left\{0;-2;6;-8\right\}\)
\(\Leftrightarrow\sqrt{x}\in\left\{0;3\right\}\)
hay \(x\in\left\{0;9\right\}\)
c) Để C nguyên thì \(\sqrt{x}-3⋮2\sqrt{x}+1\)
\(\Leftrightarrow2\sqrt{x}-6⋮2\sqrt{x}+1\)
\(\Leftrightarrow-7⋮2\sqrt{x}+1\)
\(\Leftrightarrow x\in\left\{0;9\right\}\)





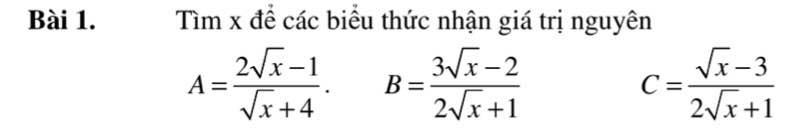






Lời giải:
a. Xét tam giác $ABM$ và $HBM$ có:
$\widehat{BAM}=\widehat{BHM}=90^0$
$\widehat{ABM}=\widehat{HBM}$ (do $BM$ là phân giác $\widehat{B}$)
$BM$ chung
$\Rightarrow \triangle ABM=\triangle HBM$ (ch-gn)
b.
Tam giác $MCH$ vuông tại $H$ nên cạnh huyền $MC$ là cạnh lớn nhất trong tam giác
$\Rightarrow MC> CH$
c.
Từ tam giác bằng nhau phần a suy ra $AM=MH$
Xét tam giác $AMK$ và $HMC$ có:
$\widehat{MAK}=\widehat{MHC}=90^0$
$AM=MH$
$\widehat{AMK}=\widehat{HMC}$ (đối đỉnh)
$\Rightarrow \triangle AMK=\triangle HMC$ (g.c.g)
$\Rightarrow MK=MC$
$\Rightarrow MKC$ cân tại $M$.
Hình vẽ: