cho tam giác cân tại A (A<90o) , đường cao AD và BE cắt nhau tại H . a) cmr 1/4AD^2=1/EB^2-1/BC^2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

AT
28 tháng 7 2021
Vì tam giác ABC cân tại A có đường cao AH nên D là trung điểm BC
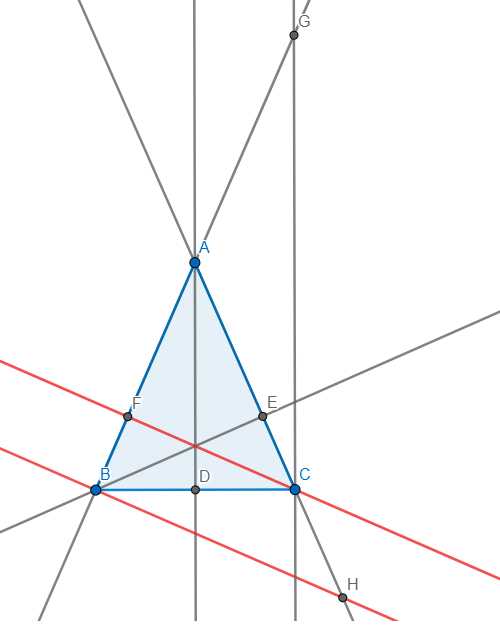
Từ C kẻ đường thẳng vuông góc với BC cắt AB tại G
\(\Rightarrow CG\parallel AD\) mà D là trung điểm BC \(\Rightarrow A\) là trung điểm BG
nên AD là đường trung bình tam giác BCG \(\Rightarrow AD=\dfrac{CG}{2}\)
\(\Rightarrow2AD=CG\Rightarrow4AD^2=CG^2\)
tam giác BCG vuông tại C có đường cao CF nên áp dụng hệ thức lượng
\(\Rightarrow\dfrac{1}{BC^2}+\dfrac{1}{CG^2}=\dfrac{1}{CF^2}\Rightarrow\dfrac{1}{BC^2}+\dfrac{1}{4AD^2}=\dfrac{1}{CF^2}\)

NT
7 tháng 4 2016
1) CH vg vs AB; AF vg góc vs =>....
2) cm tương tự a AH song song vs CF
=> hinh binh hanh