Dãy phân số nào sau đây bằng phân số \(\dfrac{15}{39}\) và và mẫu số là số tự nhiên có hai chữ số? con không hiểu đề bài này ạ, mong được chỉ giúp.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

- Ta lấy phân số tối giản của phân số đã cho:
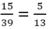
- Sau đó nhân tử và mẫu của phân số tối giản đó lần lượt với các số tự nhiên 2, 3, 4, 5, ... cho đến khi tử số và mẫu số vẫn là hai chữ số. Ta tìm được 6 phân số:
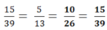
![]()

Trước tiên ta rút gọn phân số 15/39 = 5/13

Ta phải nhân cả tử và mẫu của phân số với cùng một số tự nhiên sao cho tử và mẫu của nó là các số tự nhiên có hai chữ số.

Như vậy có sáu số là 2,3,4,5,6,7 thỏa mãn yêu cầu của đề bài.

\(a.\)
\(\dfrac{-21}{39}=\dfrac{-7\cdot3}{3\cdot13}=-\dfrac{7}{13}\)
\(b.\)
\(-\dfrac{21}{39}=-\dfrac{7}{13}=-\dfrac{14}{26}=\dfrac{-28}{52}=-\dfrac{35}{65}=-\dfrac{42}{78}=-\dfrac{49}{91}\)
\(\)
a) \(-\dfrac{21}{39}=-\dfrac{21:3}{39:3}=-\dfrac{7}{13}\)
b) \(-\dfrac{21}{39}=-\dfrac{7}{13}=-\dfrac{14}{26}=-\dfrac{28}{52}=-\dfrac{35}{65}=-\dfrac{42}{78}=-\dfrac{49}{91}\)

\(\frac{30}{78},\frac{20}{52},\frac{25}{65},\frac{35}{91}\)
hết rồi nha bạn
chớ cho mik đúng

- Số tự nhiên được viết từ các chữ số 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10.
Ví dụ: 1; 4; 8; 14; 235; 10 395; ….
- Phân số được viết từ các chữ số 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10. Mỗi phân số có tử số và mẫu số. Tử số là số tự nhiên viết trên gạch ngang. Mẫu số là số tự nhiên khác 0 viết dưới gạch ngang.
Ví dụ: 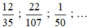
- Số thập phân cũng được viết từ các chữ số 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10. Mỗi số thập phân gồm hai phần là phần nguyên và phần thập phân, chúng được phân cách bởi dấu phẩy. Những chữ số ở bên trái dấu phẩy thuộc về phần nguyên, những chữ số ở bên phải dấu phẩy thuộc về phần thập phân.
Ví dụ: 2,5; 3,18; 10,02; …
Olm chào em, Cảm ơn em đã tin tưởng và lựa chọn gói vip của Olm. Vấn đề em hỏi, Olm xin được trả lời như sau.
Nếu đề bài cho như trên tức là em tìm trong dãy số mà đề bài đã cho các phân số thỏa mãn hai điều kiện:
Thứ nhất là mẫu của phân số đó là số tự nhiên có hai chữ số.
Thứ hai Phân số đó rút gọn thành tối giản phải bằng phân số \(\dfrac{15}{39}\);