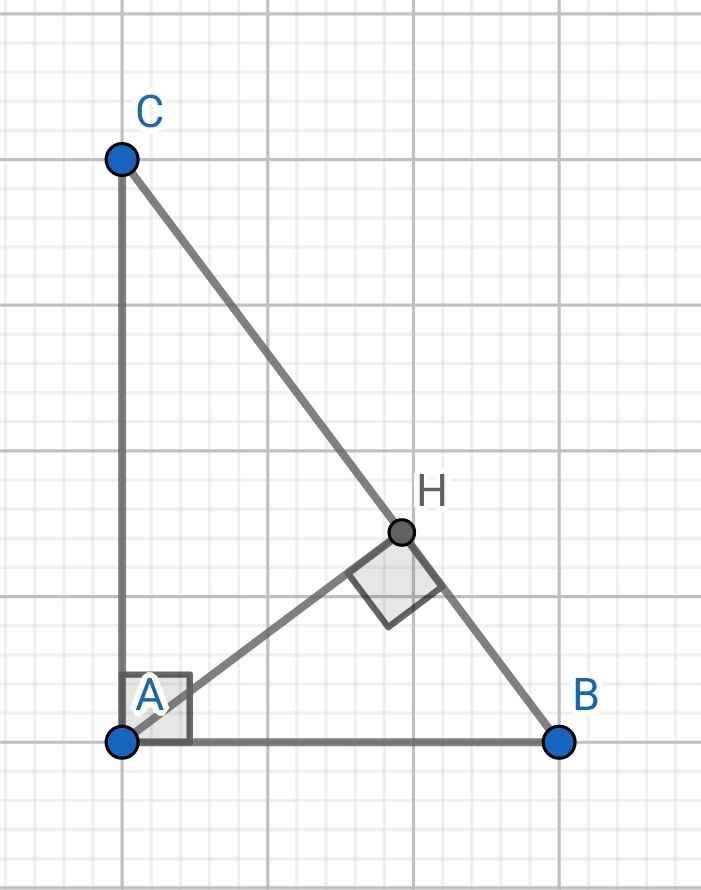
Cho tam giác ABC vuông tại A có AB=6cm, AC=8cm. Kẻ đường cao AH.
a.Chứng minh :tg ABC và tg HBA đồng dạng với nhau
b.Chứng minh: AH2 =HB.HC
c.Tính độ dài cạnh BC, AH
d.Phân giác của góc ACB cắt AH tại E, cắt AB tại D. Tính tỉ số diện tích của 2 tam giác ACD và HCE

a, Xét tam giác ABC và tam giác HBA ta có :
^ABC = ^HBA
^BAC = ^BHA = 900
Vậy tam giác ABC ~ tam giác HBA ( g.g )
b, Xét tam giác HAB và tam giác HCA ta có :
^AHB = ^CHA = 900
^BAH = ^HCA ( phụ nhau )
Vậy tam giác HAB ~ tam giác HCA ( g.g )
\(\Rightarrow\frac{AH}{CH}=\frac{BH}{AH}\Rightarrow AH^2=BH.CH\)
c, Áp dụng định lí Pytago cho tam giác ABC vuông tại A
\(AB^2+AC^2=BC^2\Rightarrow BC^2=36+64\Rightarrow BC=10\)cm
Vì tam giác ABC ~ tam giác HBA ( cma )
\(\Rightarrow\frac{AC}{AH}=\frac{BC}{AB}\)( tỉ lệ thức )
\(\Rightarrow AH=\frac{AB.AC}{BC}=\frac{6.8}{10}=\frac{48}{10}=\frac{24}{5}\)cm