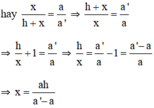Có một công viên nhỏ hình tam giác như Hình 1. Người ta dự định đặt một cây đèn để chiếu sáng toàn bộ công viên. Để công việc tiến hành thuận lợi, người ta đo đạc và mô phông các kích thước công viên như Hình 2. Thiết lập một hệ trục Oxy như Hình 3, khi đó các đỉnh của công viên có tọa độ lần lượt là A (0:3), B(4:0), C(4:7). Gọi 1 là điểm đặt cây đèn sao cho đèn chiếu sáng toàn bộ công viên. Vậy cần đặt 1 ở vị trí có tọa độ bao nhiêu?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

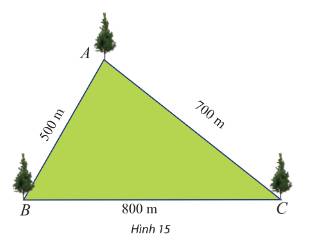
Đặt \(a = BC,b = AC,c = AB\)
Ta có: \(a = 800,b = 700,c = 500.\)
Áp dụng định lí cosin, ta có:
\(\cos A = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}};\cos B = \frac{{{a^2} + {c^2} - {b^2}}}{{2ac}};\cos C = \frac{{{a^2} + {b^2} - {c^2}}}{{2ab}}.\)
Suy ra:
\(\begin{array}{l}\cos A = \frac{{{{700}^2} + {{500}^2} - {{800}^2}}}{{2.700.500}} = \frac{1}{7} \Rightarrow \widehat A = {81^o}47'12,44'';\\\cos B = \frac{{{{500}^2} + {{800}^2} - {{700}^2}}}{{2.500.800}} = \frac{1}{2} \Rightarrow \widehat B = {60^o};\\\cos C = \frac{{{{800}^2} + {{700}^2} - {{500}^2}}}{{2.800.700}} = \frac{{11}}{{14}} \Rightarrow \widehat C = {38^o}12'47,56''.\end{array}\)
Vậy \(\widehat A = {81^o}47'12,44'';\widehat B = {60^o};\widehat C = {38^o}12'47,56''.\)

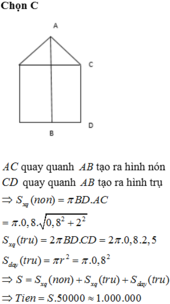
Đáp án C
Khi quay cạnh AB quanh trục AB ta được hình nón có bán kính đáy r = 0,8 cm


a) Diện tích căn phòng là : 6 x 8 = 48 ( m2 ) = 4800 ( dm2 )
Diện tích viên gạch là : 4 x 4 = 16 ( dm2 )
Số viên gạch cần để lát nền căn phòng là : 4800 : 16 = 300 ( viên )
b) Số tiền cần để mua gạch lát nền là : 48 x 120000 = 5760000 ( đồng )
Đ/S : a) 300 viên gạch
b) 5760000 đồng .

Chiều rộng công viên:
140 - 70 = 70 (m)
a, Diện tích công viên:
140 x 70 = 9800 (m2)
b, Diện tích còn lại:
9800 x (100% - 50%) = 4900 (m2)
Đ.số:......

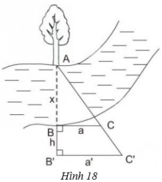
+ Mô tả cách làm:
- Chọn một điểm A cố định bên mép bờ sông bên kia (chẳng hạn như là một thân cây), đặt hai điểm B và B' thẳng hàng với A, điểm B sát mép bờ còn lại và AB chính là khoảng cách cần đo.
- Trên hai đường thẳng vuông góc với AB' tại B và B' lấy C và C' thằng hàng với A.
- Đo độ dài các đoạn BB' = h, BC = a, B'C' = a' ta sẽ tính được đoạn AB.
+ Cách tính AB.
Ta có: BC ⊥ AB’ và B’C’ ⊥ AB’ ⇒ BC // B’C’
ΔAB’C’ có BC // B’C’ (B ∈ AB’, C ∈ AC’)
⇒ 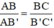 (hệ quả định lý Talet)
(hệ quả định lý Talet)