Cho A nằm trong \(\widehat{xOy}\) nhọn. Tìm điểm B,C lần lượt thuộc Ox, Oy sao cho \(\Delta ABC\) có chu vi nhỏ nhất
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
18 tháng 8 2019
+ Xét tam giác bất kì ABC có Bvà C lần lượt nằm trong hai tia Ox và Oy
+ Gọi A' và A'' là các điểm đối xứng với điểm A lần lượt qua các đường thẳng Ox và Oy .
Ta có \(AB=A'B\) và \(AC=A'CC\)( do các tam giác \(ABA'\)và tam giác \(ACA''\)là tam giác cân).
+ Gọi 2p là chu vi của tam giác ABC thì có :
2p = \(AB+BC+CA=A'B+BC+CA''\ge A'A''\)
Dấu'' bằng '' xảy ra khi 4 điểm \(A'B,C,A''\)thẳng hàng .
Nên để chu vi tam giác ABC bé nhất thì phải lấy B và lần lượt là giao điểm của đoạn thẳng \(A'A''\)với hai tia Ox và Oy ( các giao điểm đó tồn tại vì góc xOy nhọn )
Chúc bạn học tốt !!!
CM
31 tháng 12 2017
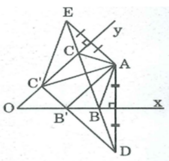
Cách dựng:
- Dựng điểm D đối xứng với A qua Ox
- Dựng điểm E đối xứng với A qua Oy
Nối DE cắt Ox tại B, Oy tại C
Tam giác ABC là tam giác có chu vi nhỏ nhất
Vì ∠ (xOy) < 90 0 nên DE luôn cắt Ox và Oy do đó ∆ ABC luôn dựng được.
Chứng minh:
Chu vi ∆ ABC bằng AB + BC + AC
Vì D đối xứng với A qua Ox nên Ox là trung trực của AD
⇒ AB = BD (tính chất đường trung trực)
E đối xứng với A qua Oy nên Oy là trung trực của AE
⇒ AC = CE (tính chất đường trung trực)
Suy ra: AB + BC + AC = BD + BC + BE = DE (1)
Lấy B' bất kì trên Ox, C' bất kì trên tia Oy. Nối C'E, C'A, B'A, B'D.
Ta có: B'A = B'D và C'A = C'E (tính chất đường trung trực)
Chu vi ∆ AB'C' bằng AB'+ AC’ + B'C'= B'D+C’E+ B'C' (2)
Vì DE ≤ B'D + C’E+ B'C' (dấu bằng xảy ra khi B' trùng B, C' trùng C) nên chu vi của ∆ ABC ≤ chu vi của ∆ A'B'C'
Vậy ∆ ABC có chu vi bé nhất.
4 tháng 8 2016
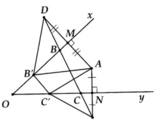
Lấy M, N lần lượt là điểm đối xứng với A qua Ox và Oy
Ta có: P(ABC)=AB+AC+BC=BM+BC+CN≥MNP(ABC)=AB+AC+BC=BM+BC+CN≥MN
Dấu bằng xảy ra khi M,B,C,N thẳng hàng
Vậy chu vi tam giác ABC nhỏ nhất khi B,C thuộc MN
Lấy \(A_1\) đối xứng A qua Ox và \(A_2\) đối xứng A qua Oy
\(\Rightarrow Ox\) là trung trực của \(AA_1\) và Oy là trung trực của \(AA_2\)
Do B thuộc Ox \(\Rightarrow AB=A_1B\)
Do C thuộc Oy \(\Rightarrow AC=A_2C\)
\(\Rightarrow AB+AC+BC=A_1B+BC+A_2C\ge A_1A_2\)
Dấu "=" xảy ra khi \(A_1;B;C;A_2\) thẳng hàng hay \(B;C\) lần lượt là giao điểm của \(A_1A_2\) với Ox và Oy