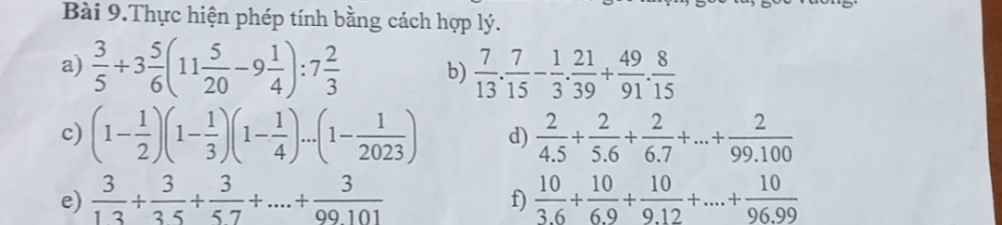 giup em may bai nay em cam on aj
giup em may bai nay em cam on aj
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Cách làm ngắn gọn: \(5=\dfrac{5\left(x-1\right)}{x-1}=\dfrac{5x-5}{x-1}=\dfrac{5x+5-10}{x-1}\)
Do đó chọn \(f\left(x\right)=5x+5\) thế vào nhanh chóng tính ra kết quả giới hạn
Còn cách khác phức tạp hơn (có thể sử dụng cho tự luận):
Do \(\lim\limits_{x\rightarrow1}\dfrac{f\left(x\right)-10}{x-1}=5\) hữu hạn nên \(f\left(x\right)-10=0\) có nghiệm \(x=1\)
\(\Rightarrow f\left(1\right)-10=0\Rightarrow f\left(1\right)=10\)
Do đó:
\(\lim\limits_{x\rightarrow1}\dfrac{f\left(x\right)-10}{\left(\sqrt{x}-1\right)\left(\sqrt{4f\left(x\right)+9}+3\right)}=\lim\limits_{x\rightarrow1}\dfrac{\left[f\left(x\right)-10\right]\left(\sqrt{x}+1\right)}{\left(x-1\right)\left(\sqrt{4f\left(x\right)+9}+3\right)}\)
\(=\lim\limits_{x\rightarrow1}\dfrac{f\left(x\right)-10}{x-1}.\dfrac{\sqrt{x}+1}{\sqrt{4f\left(x\right)+9}+3}=5.\dfrac{1+1}{\sqrt{4f\left(1\right)+9}+3}=5.\dfrac{2}{\sqrt{4.10+9}+3}=...\)


\(\frac{1}{1.4}+\frac{1}{4.7}+\frac{1}{7.10}+...+\frac{1}{40.43}+\frac{1}{43.46}\)
\(=3.\left(1-\frac{1}{4}+\frac{1}{4}-\frac{1}{7}+\frac{1}{7}-\frac{1}{10}+...+\frac{1}{43}-\frac{1}{46}\right)\)
\(=3.\left(1-\frac{1}{46}\right)\)
\(=3.\frac{45}{46}\)
\(=\frac{135}{46}\)
~Học tốt~


Câu 2:
a: Không
b: Không
Câu 3:
a: \(\widehat{B}=\widehat{zAB}\left(=124^0\right)\)
mà hai góc này là hai góc ở vị trí so le trong
nên Bt//Az
b: n\(\perp\)DC
m\(\perp\)DC
Do đó: n//m
c: \(\widehat{xEG}+\widehat{yGE}=70^0+110^0=180^0\)
mà hai góc này là hai góc ở vị trí trong cùng phía
nên Ex//Gy
d: Vẽ lại hình, ta sẽ có:
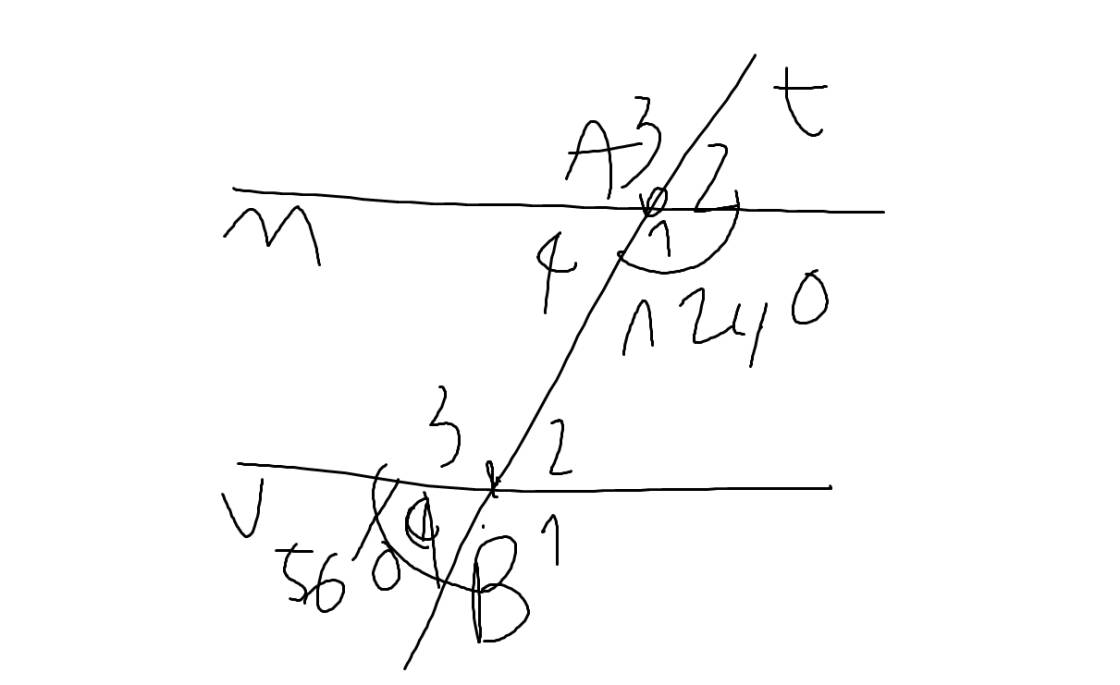
Ta có: \(\widehat{B_4}=\widehat{B_2}\)(hai góc đối đỉnh)
mà \(\widehat{B_4}=56^0\)
nên \(\widehat{B_2}=56^0\)
Ta có: \(\widehat{A_1}+\widehat{B_2}=124^0+56^0=180^0\)
mà hai góc này là hai góc ở vị trí trong cùng phía
nên m//v




 may bai nay kho qua giup em , em dang can gap a
may bai nay kho qua giup em , em dang can gap a
a: \(\dfrac{3}{5}+3\dfrac{5}{6}\left(11\dfrac{5}{20}-9\dfrac{1}{4}\right):7\dfrac{2}{3}\)
\(=\dfrac{3}{5}+\dfrac{23}{6}\left(11+\dfrac{5}{20}-9-\dfrac{1}{4}\right):\dfrac{23}{3}\)
\(=\dfrac{3}{5}+\dfrac{23}{6}\cdot2\cdot\dfrac{3}{23}=\dfrac{3}{5}+1=\dfrac{8}{5}\)
b: \(\dfrac{7}{13}\cdot\dfrac{7}{15}-\dfrac{1}{3}\cdot\dfrac{21}{39}+\dfrac{49}{91}\cdot\dfrac{8}{15}\)
\(=\dfrac{7}{13}\cdot\dfrac{7}{15}-\dfrac{1}{3}\cdot\dfrac{7}{13}+\dfrac{7}{13}\cdot\dfrac{8}{15}\)
\(=\dfrac{7}{13}\left(\dfrac{7}{15}+\dfrac{8}{15}-\dfrac{1}{3}\right)=\dfrac{7}{13}\cdot\dfrac{2}{3}=\dfrac{14}{39}\)
c: \(\left(1-\dfrac{1}{2}\right)\left(1-\dfrac{1}{3}\right)\cdot...\cdot\left(1-\dfrac{1}{2023}\right)\)
\(=\dfrac{1}{2}\cdot\dfrac{2}{3}\cdot...\cdot\dfrac{2022}{2023}\)
\(=\dfrac{1}{2023}\)
d: \(\dfrac{2}{4\cdot5}+\dfrac{2}{5\cdot6}+...+\dfrac{2}{99\cdot100}\)
\(=2\left(\dfrac{1}{4\cdot5}+\dfrac{1}{5\cdot6}+...+\dfrac{1}{99\cdot100}\right)\)
\(=2\left(\dfrac{1}{4}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{6}+...+\dfrac{1}{99}-\dfrac{1}{100}\right)\)
\(=2\left(\dfrac{1}{4}-\dfrac{1}{100}\right)=2\cdot\dfrac{24}{100}=\dfrac{48}{100}=\dfrac{12}{25}\)
e: \(\dfrac{3}{1\cdot3}+\dfrac{3}{3\cdot5}+...+\dfrac{3}{99\cdot101}\)
\(=\dfrac{3}{2}\left(\dfrac{2}{1\cdot3}+\dfrac{2}{3\cdot5}+...+\dfrac{2}{99\cdot101}\right)\)
\(=\dfrac{3}{2}\left(1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+...+\dfrac{1}{99}-\dfrac{1}{101}\right)\)
\(=\dfrac{3}{2}\left(1-\dfrac{1}{101}\right)=\dfrac{3}{2}\cdot\dfrac{100}{101}=\dfrac{150}{101}\)
f: \(\dfrac{10}{3\cdot6}+\dfrac{10}{6\cdot9}+...+\dfrac{10}{96\cdot99}\)
\(=\dfrac{10}{3}\left(\dfrac{3}{3\cdot6}+\dfrac{3}{6\cdot9}+...+\dfrac{3}{96\cdot99}\right)\)
\(=\dfrac{10}{3}\left(\dfrac{1}{3}-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{9}+...+\dfrac{1}{96}-\dfrac{1}{99}\right)\)
\(=\dfrac{10}{3}\left(\dfrac{1}{3}-\dfrac{1}{99}\right)=\dfrac{10}{3}\cdot\dfrac{32}{99}=\dfrac{320}{297}\)