 giúp mình v
giúp mình v
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


11) \(\dfrac{2\sqrt{3}-\sqrt{15}}{\sqrt{3}}\)
\(=\dfrac{\left(2\sqrt{3}-\sqrt{15}\right)\sqrt{3}}{\sqrt{3}\cdot\sqrt{3}}\)
\(=\dfrac{2\cdot\sqrt{3}\cdot\sqrt{3}-\sqrt{15}\cdot\sqrt{3}}{3}\)
\(=\dfrac{6-3\sqrt{5}}{3}\)
\(=2-\sqrt{5}\)
12) \(\dfrac{2\sqrt{2}+\sqrt{2}}{5\sqrt{2}}\)
\(=\dfrac{3\sqrt{2}}{5\sqrt{2}}\)
\(=\dfrac{3}{5}\)
11: \(=\dfrac{\sqrt{3}\left(2-\sqrt{5}\right)}{\sqrt{3}}=2-\sqrt{5}\)
12: \(=\dfrac{3\sqrt{2}}{5\sqrt{2}}=\dfrac{3}{5}\)

\(8.\dfrac{\sqrt{3}}{\sqrt{2}}=8.\dfrac{\sqrt{3}.\sqrt{2}}{\sqrt{2}.\sqrt{2}}=8.\dfrac{\sqrt{6}}{2}=4\sqrt{6}\)

99 - 97 + 95 - 93 + 91 - 89 + ... + 7 - 5
= ( 99 - 97 ) + ( 95 - 93 ) + ( 91 - 89 ) + ... + ( 7 - 5 )
= 2 + 2 + 2 + ... + 2
Dãy số trên có số cặp là :
[ ( 99 - 5 ) : 2 + 1 ] : 2 = 24 ( cặp )
\(\Rightarrow\) 2 . 24 = 48
Vậy phép tính trên = 48 .

sorry mình lười type quá cơ mà cái này là bước cơ bản quan trọng để bạn làm được bài chuyển đổi chủ động sang bị động ý ạ :))) nên bạn thử tham khảo thêm lí thuyết rồi làm thử xem sao ha, nếu bạn làm xong có thể gửi mình check cho =))

1 The teacher asked us not to make so much noise
2 She asked me to give her an English book
3 Mr Quang drives carefully
4 I used to live in the village when I was a child
5 The doctor advised me not to eat so much fatty food
6 Hoa is the same weight as Hoa
7 My favorite food is fruit
8 Phong is younger than Ba


Bài 6:
a: ĐKXĐ: \(\left\{{}\begin{matrix}x>=0\\x\notin\left\{4;9\right\}\end{matrix}\right.\)
b: \(C=\left(1-\dfrac{x-3\sqrt{x}}{x-9}\right):\left(\dfrac{\sqrt{x}-3}{2-\sqrt{x}}+\dfrac{\sqrt{x}-2}{3+\sqrt{x}}-\dfrac{9-x}{x+\sqrt{x}-6}\right)\)
\(=\dfrac{x-9-x+3\sqrt{x}}{x-9}:\left(\dfrac{-\left(\sqrt{x}-3\right)}{\left(\sqrt{x}-2\right)}+\dfrac{\sqrt{x}-2}{\sqrt{x}+3}+\dfrac{x-9}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}\right)\)
\(=\dfrac{3\sqrt{x}-9}{x-9}:\left(\dfrac{-\left(\sqrt{x}-3\right)}{\sqrt{x}-2}+\dfrac{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}+\dfrac{\sqrt{x}-2}{\sqrt{x}+3}\right)\)
\(=\dfrac{3\left(\sqrt{x}-3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}:\left(\dfrac{-\left(\sqrt{x}-3\right)}{\sqrt{x}-2}+\dfrac{\sqrt{x}-3}{\sqrt{x}-2}+\dfrac{\sqrt{x}-2}{\sqrt{x}+3}\right)\)
\(=\dfrac{3}{\sqrt{x}+3}:\dfrac{\sqrt{x}-2}{\sqrt{x}+3}=\dfrac{3}{\sqrt{x}-2}\)
c: C=4
=>\(\sqrt{x}-2=\dfrac{3}{4}\)
=>\(\sqrt{x}=2+\dfrac{3}{4}=\dfrac{11}{4}\)
=>\(x=\left(\dfrac{11}{4}\right)^2=\dfrac{121}{16}\left(nhận\right)\)
Câu 5:
a: ĐKXĐ: x>=0 và x<>1
b: \(B=\left(\dfrac{x+2\sqrt{x}}{x\sqrt{x}-1}-\dfrac{1}{\sqrt{x}-1}\right):\dfrac{x-1}{x+\sqrt{x}+1}\)
\(=\left(\dfrac{x+2\sqrt{x}}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}-\dfrac{1}{\sqrt{x}-1}\right)\cdot\dfrac{x+\sqrt{x}+1}{x-1}\)
\(=\dfrac{x+2\sqrt{x}-x-\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\cdot\dfrac{x+\sqrt{x}+1}{x-1}\)
\(=\dfrac{\sqrt{x}-1}{\sqrt{x}-1}\cdot\dfrac{1}{x-1}=\dfrac{1}{x-1}\)

III - II = I
X + X = XX
IV + V = IX
XXII - XX = II
V - I = IV

a)2011.2013=2011.(2012+1)=2011.2012+2011
và 2012.2012=2012.2011+2012
2011.2012+2011<2012.2011+2012
Từ đó suy ra 2011.2013<2012.2012
b)2002.2002=2002.(2000+2)=2002.2000+2002.2
và 2000.2004=2000.(2002+2)=2000.2002+2000.2
2002.2000+2002.2>2000.2002+2000.2
Từ đó suy ra 2002.2002>2000.2004

1 would receive
2 is
3 were
4 have
5 will watch
6 wouldn't be
7 will get
8 works
9 were
10 rains
 giúp mình câu 11 , 12 v ạ mình camon
giúp mình câu 11 , 12 v ạ mình camon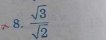 trục căn thức ở mẫu giúp mình v ạ mình camonn
trục căn thức ở mẫu giúp mình v ạ mình camonn



a: Xét ΔMAB và ΔMCI có
MA=MC
\(\widehat{AMB}=\widehat{CMI}\)(hai góc đối đỉnh)
MB=MI
Do đó: ΔMAB=ΔMCI
b: ta có: ΔMAB=ΔMCI
=>\(\widehat{MAB}=\widehat{MCI}\)
mà \(\widehat{MAB}=90^0\)
nên \(\widehat{MCI}=90^0\)
=>CI\(\perp\)AC
Ta có: ΔMAB=ΔMCI
=>AB=CI
mà AB<CB
nên CI<CB
Xét ΔCIB có \(\widehat{CBI};\widehat{CIB}\) lần lượt là góc đối diện của các cạnh CI,CB
mà CI<CB
nên \(\widehat{CBI}< \widehat{CIB}\)
c: Ta có: KC+CM=KM
=>\(KM=CA+\dfrac{1}{2}CA=\dfrac{3}{2}CA=\dfrac{3}{2}KC\)
=>\(KC=\dfrac{2}{3}KM\)
Xét ΔKIB có
KM là đường trung tuyến
\(KC=\dfrac{2}{3}KM\)
Do đó: C là trọng tâm của ΔKIB
=>IC đi qua trung điểm của BK