Cho hàm số f(x) = \(\sqrt{x^2-2x}\). Tập nghiệm S của bất phương trình f'(x) ≥f(x) có bao nhiêu giá trị nguyên?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

CM
31 tháng 12 2017
Chọn A.
Ta có: f(x + 1) = log2x
Khi đó f(x + 1) > 1 khi và chỉ khi log2x > 1 hay x > 2.

CM
21 tháng 10 2019
Chọn B.
Ta có: f(x + 1) = log2(x + 1) và g(x + 2) = log2(2 - x)
![]()
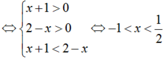

CM
18 tháng 12 2018
Đáp án C.
- Phương pháp:
+) Tính f'(x).
+) Sử dụng quy tắc trong trái ngoài cùng giải bất phương trình bậc hai.
- Cách giải:
+ Ta có:
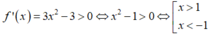
→ Vậy tập nghiệm của bất phương trình là 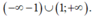

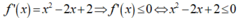
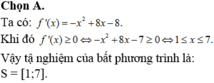
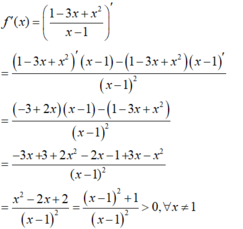

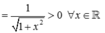
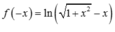
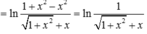
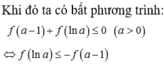
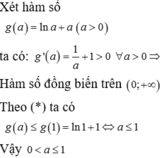
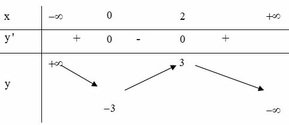
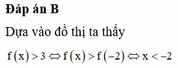
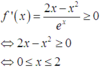
ĐKXĐ: \(\left[{}\begin{matrix}x\ge2\\x\le0\end{matrix}\right.\)
\(f'\left(x\right)=\dfrac{x-1}{\sqrt{x^2-2x}}\)
\(f'\left(x\right)\ge f\left(x\right)\Leftrightarrow\dfrac{x-1}{\sqrt{x^2-2x}}\ge\sqrt{x^2-2x}\)
\(\Rightarrow x-1\ge x^2-2x\)
\(\Rightarrow x^2-3x+1\le0\)
\(\Rightarrow\dfrac{3-\sqrt{5}}{2}\le x\le\dfrac{3+\sqrt{5}}{2}\)
Kết hợp ĐKXĐ \(\Rightarrow2\le x\le\dfrac{3+\sqrt{5}}{2}\)
\(\Rightarrow x=2\) là giá trị nguyên duy nhất thỏa mãn