cho tam giác HMN có góc ngoài đỉnh H bằng 160 độ,xắp xếp các cạnh theo thứ tự tăng dần
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
4 tháng 8 2023
\(a,-\dfrac{3}{2};-\dfrac{2}{3};0;\dfrac{4}{7};\dfrac{2}{3}\\ b,\dfrac{4}{3};\dfrac{4}{5};0,2;-\dfrac{5}{2}\)
HQ
Hà Quang Minh
Giáo viên
19 tháng 9 2023
- AB < AC < BC nên sắp xếp độ dài các cạnh theo thứ tự từ bé đến lớn là: AB, AC, BC.
\(\widehat C < \widehat B < \widehat A\) nên sắp xếp độ lớn các góc theo thứ tự từ bé đến lớn là: \(\widehat C;\widehat B;\widehat A\)
- Góc lớn nhất là góc A đối diện với cạnh BC. Góc bé nhất là góc C đối diện với cạnh AB.
TN
2
HH
2
17 tháng 9 2023
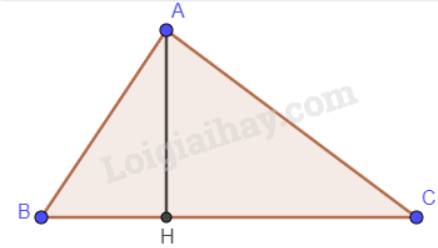
Xét tam giác ABC có: H là hình chiếu của A lên BC nên \(AH \bot BC\). Vậy AH < AB, AC.
Mà trong tam giác ABC có \(\widehat B > \widehat C\)nên AC > AB (AC đối diện với góc B; AB đối diện với góc C).
Các đoạn thẳng AB, AH, AC theo thứ tự độ dài tăng dần là: AH, AB, AC.
3N
1
YN
12 tháng 2 2023
Quy đồng các phân số đã cho lên, ta được:
\(\dfrac{3}{4}=\dfrac{3\times42}{4\times42}=\dfrac{126}{168}\)
\(\dfrac{5}{6}=\dfrac{5\times28}{6\times28}=\dfrac{140}{168}\)
\(\dfrac{11}{8}=\dfrac{11\times21}{8\times21}=\dfrac{231}{168}\)
\(\dfrac{8}{7}=\dfrac{8\times24}{7\times24}=\dfrac{192}{168}\)
\(5=\dfrac{5}{1}=\dfrac{5\times168}{1\times168}=\dfrac{840}{168}\)
Mà \(\dfrac{840}{168}>\dfrac{231}{168}>\dfrac{192}{168}>\dfrac{140}{168}>\dfrac{126}{168}\)
Vậy ta sắp xếp được các phân số theo thứ tự tăng dần là: \(\dfrac{3}{4};\dfrac{5}{6};\dfrac{8}{7};\dfrac{11}{8};5\).
N
2
NK
2
TT
17 tháng 8 2021
P,N,O
Ta có: P và N cùng thuộc nhóm VA, theo quy luật biến đổi xác định được tính phi kim của P < N. O và N cùng thuộc chu kỳ 2, theo quy luật biến đổi xác định được tính phi kim của N < O. Chiều tăng dần tính phi kim là: P < N < O.
17 tháng 8 2021
Cho các nguyên tố sau: N, P, O. Hãy chỉ ra thứ tự sắp xếp đúng theo chiều tính phi kim tăng dần.
Chiều tăng dần tính phi kim là: P < N < O.
P và N cùng thuộc nhóm VA, theo quy luật biến đổi xác định được tính phi kim của P < N.
O và N cùng thuộc chu kỳ 2, theo quy luật biến đổi xác định được tính phi kim của N < O.
Đề thiếu số đo một góc