Giải phương trình �2−5�+6=0x2−5x+6=0 và cho biết nghiệm của phương trình là...
Đọc tiếp
Giải phương trình và cho biết nghiệm của phương trình là gì.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
0
26 tháng 3 2018
a. Thay x = 2 vào vế trái của phương trình (1), ta có:
22 – 5.2 + 6 = 4 – 10 + 6 = 0
Vế trái bằng vế phải nên x = 2 là nghiệm của phương trình (1).
Thay x = 2 vào vế trái của phương trình (2), ta có:
2 + (2 – 2)(2.2 +1) = 2 + 0 = 2
Vế trái bằng vế phải nên x = 2 là nghiệm của phương trình (2).
Vậy x = 2 là nghiệm chung của hai phương trình (1) và (2).
b. Thay x = 3 vào vế trái của phương trình (1), ta có:
32 – 5.3 + 6 = 9 – 15 + 6 = 0
Vế trái bằng vế phải nên x = 3 là nghiệm của phương trình (1).
Thay x = 3 vào vế trái của phương trình (2), ta có:
3 + (3 – 2)(2.3 + 1) = 3 + 7 = 10 ≠ 2
Vì vế trái khác vế phải nên x = 3 không phải là nghiệm của phương trình (2).
Vậy x = 3 là nghiệm của phương trình (1) nhưng không phải là nghiệm của phương trình (2).
c. Hai phương trình (1) và (2) không tương đương nhau vì x = 3 không phải là nghiệm chung của hai phương trình.
CM
6 tháng 8 2017
Chọn B.
Ta có:
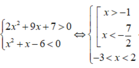
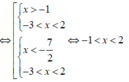
Vậy tập nghiệm hệ bất phương trình là S = (-1;2).
NV
Nguyễn Việt Lâm
Giáo viên
9 tháng 9 2021
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{5}{3}\\x_1x_2=-2\end{matrix}\right.\)
Ta có: \(\left\{{}\begin{matrix}y_1+y_2=2x_1-x_2+2x_2-x_1\\y_1y_2=\left(2x_1-x_2\right)\left(2x_2-x_1\right)\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}y_1+y_2=x_1+x_2\\y_1y_2=-2x_1^2-2x_2^2+5x_1x_2\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}y_1+y_2=-\dfrac{5}{3}\\y_1y_2=-2\left(x_1+x_2\right)^2+9x_1x_2\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}y_1+y_2=-\dfrac{5}{3}\\y_1y_2=-2.\left(-\dfrac{5}{3}\right)^2+9.\left(-2\right)=-\dfrac{212}{9}\end{matrix}\right.\)
\(\Rightarrow y_1;y_2\) là nghiệm của:
\(y^2+\dfrac{5}{3}y-\dfrac{212}{9}=0\Leftrightarrow9y^2+10y-212=0\)
HN
1 tháng 1 2022
Giải thích các bước giải:
a.Với m=6→x2−5x+6=0→(x−2)(x−3)=0→x∈{2,3}m=6→x2−5x+6=0→(x−2)(x−3)=0→x∈{2,3}
b.Để phương trình có 2 nghiệm x1,x2x1,x2
→Δ=52−4m≥0→m≤254→Δ=52−4m≥0→m≤254
→{x1+x2=5x1x2=m→{x1+x2=5x1x2=m
Mà |x1−x2|=3→(x1−x2)2=9|x1−x2|=3→(x1−x2)2=9
→(x1+x2)2−4x1x2=9→(x1+x2)2−4x1x2=9
→52−4m=9→52−4m=9
→m=−4
1 tháng 1 2022
a, khi m=6 thì pt\(\Leftrightarrow x^2-5x+6=0\)
\(\Leftrightarrow\left(x^2-2x\right)-\left(3x-6\right)=0\\ \Leftrightarrow x\left(x-2\right)-3\left(x-2\right)=0\\ \Leftrightarrow\left(x-2\right)\left(x-3\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=2\\x=3\end{matrix}\right.\)
b,Ta có:\(\Delta=\left(-5\right)^2-4.1.m=25-4m\)
để pt có 2 nghiệm x1, x2 phân biệt thì \(\Delta>0\) hay \(25-4m>0\Rightarrow m< \dfrac{25}{4}\)
YN
11 tháng 2 2023
a)
\(m=6\)
\(\Rightarrow x^2+5x+6=0\)
\(\Leftrightarrow\left(x+2\right)\left(x+3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+2=0\\x+3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-2\\x=-3\end{matrix}\right.\)
b)
\(\left|x_1-x_2\right|=3\)
\(\Leftrightarrow\left(x_1-x_2\right)^2=9\)
\(\Leftrightarrow x_1^2=2x_1x_2+x^2_2=9\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-4x_1x_2=9\)
Mà \(\left\{{}\begin{matrix}x_1+x_2=-5\\x_1-x_2=m\end{matrix}\right.\)
\(\Rightarrow25-4m=9\)
\(\Leftrightarrow4m=16\)
\(\Leftrightarrow m=4\)
x² - 5x + 6 = 0
x² - 2x - 3x + 6 = 0
(x² - 2x) - (3x - 6) = 0
x(x - 2) - 3(x - 2) = 0
(x - 2)(x - 3) = 0
x - 2 = 0 hoặc x - 3 = 0
*) x - 2 = 0
x = 2
*) x - 3 = 0
x = 3
Vậy S = {2; 3}