cho tam giác HMN có số đo góc ngoài đỉnh h bằng 160 độ . sắp xếp các cạnh của tam giác HMN rheo thứ tự tăng dần
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


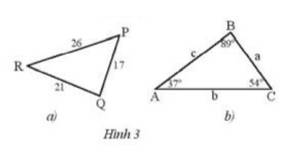
a) Ta có độ dài các cạnh tam giác PQR theo thứ tự từ nhỏ đến lớn là PQ, QR, RP
Vì trong tam giác góc đối diện cạnh lớn hơn thì lớn hơn
Nên ra có các góc tam giác PQR theo thứ tự từ nhỏ đến lớn là R, P, Q
b) Ta có số đo các góc theo tứ tự từ nhỏ đến lớn của tam giác ABC là A, C, B
Vì trong tam giác góc đối diện cạnh lớn hơn thì lớn hơn
Nên ta có các cạnh tam giác ABC theo thứ tự từ nhỏ đến lớn là a, c, b.

a) \(BM.CN=\dfrac{a^2}{4}=\dfrac{a}{2}.\dfrac{a}{2}=\dfrac{BC}{2}.\dfrac{BC}{2}=BH.HC\)
\(\Rightarrow\dfrac{BM}{BH}=\dfrac{HC}{CN}\)\(\Rightarrow\)△BMH∼△CHN (c-g-c)
\(\Rightarrow\widehat{BMH}=\widehat{CHN}\)
\(\widehat{MHN}=180^0-\widehat{BHM}-\widehat{CHN}=180^0-\widehat{BHM}-\widehat{BMH}=\widehat{MBH}=60^0\)
b) △BMH∼△CHN \(\Rightarrow\dfrac{BM}{CH}=\dfrac{MH}{HN}\Rightarrow\dfrac{BM}{BH}=\dfrac{MH}{HN}\)
\(\Rightarrow\)△HMN∼△BMH (c-g-c)
c) \(\Rightarrow\widehat{HMN}=\widehat{BMH}\)\(\Rightarrow\)MH là p/g góc BMN.

Bài 1:
Số đo góc ngoài tại đỉnh C là \(74^0+47^0=121^0\)
Câu 2:
Đặt \(\widehat{D}=a;\widehat{E}=b\)
Theo đề, ta có hệ phương trình:
\(\left\{{}\begin{matrix}a-b=52\\a+b=140\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=96\\b=44\end{matrix}\right.\)
Bài 3:
Theo đề, ta có: x+2x+3x=180
=>6x=180
=>x=30
=>\(\widehat{A}=30^0;\widehat{B}=60^0;\widehat{C}=90^0\)

a. B = 55 độ
C = 35
b. lỗi. phải là 360 độ
ông họ ngô
tôi họ đinh

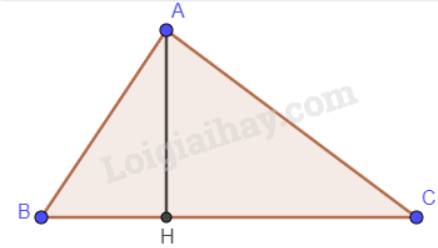
Xét tam giác ABC có: H là hình chiếu của A lên BC nên \(AH \bot BC\). Vậy AH < AB, AC.
Mà trong tam giác ABC có \(\widehat B > \widehat C\)nên AC > AB (AC đối diện với góc B; AB đối diện với góc C).
Các đoạn thẳng AB, AH, AC theo thứ tự độ dài tăng dần là: AH, AB, AC.

Đáp án B.
Gọi I là trung điểm của SP. Theo định lý Talet:
d 1 H M N = 1 2 d S H M N . Ta cần tính d S H M N .
Bước 1: Tìm V S . H M N
Ta có:
V S . H M N V S . H A D = 1 2 . 1 2 = 1 4 ; V S . H A D V S . A B C D = 1 4
Giả sử a = 1
Dễ thấy
V S . A B C D = 1 3 S H . S A B C D = 1 3 . 3 2 . 3 2 = 1 4
⇒
V
S
.
H
M
N
=
1
16
.
1
4
=
1
64
.
Bước 2: Tìm S H M N . Ta có: M H → = − 1 2 B S → và M N → = 1 2 B C → ⇒ H M N = 180 ° − S B C .
Do đó
sin H M N = sin S B C ⇒ S H M N = 1 2 M H . M N . sin H M N = 1 4 . S S B C .
Tam giác SBC có SB = BC = 1;
S C = S H 2 + H C 2 = 2 S H = 6 2 ⇒ S S B C = 15 8 .
Do đó S H M N = 1 4 . 15 8 = 15 32 .
Bước 3: Sử dụng công thức:
d S H M N = 3. V S . H M N S H M N = 3 64 . 32 15 = 15 10 ⇒ d I H M N = 1 2 . 15 10 = 15 20 .

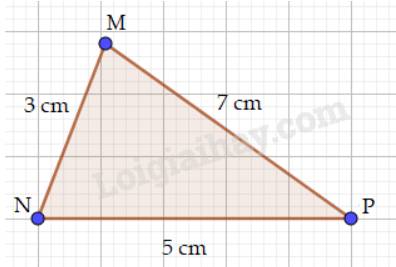
Góc P đối diện với cạnh MN
Góc M đối diện với cạnh NP
Góc N đối diện với cạnh MP.
Ta có: MN < NP < MP nên \(\widehat P < \widehat M < \widehat N\)( định lí)
Vậy sắp xếp các góc của tam giác MNP theo thứ tự từ bé đến lớn là: \(\widehat P;\widehat M;\widehat N\).

a: góc BAC=180-120=60 độ
góc ABE=70/2=35 độ
góc AEB=180-60-35=85 độ
b: góc ABE<góc BAE<góc AEB
=>AE<BE<AB
c: góc ECB=180-70-60=50 độ
góc BEC=180-85=95 độ
Vì góc EBC<góc ECB<góc BEC
nên EC<EB<BC

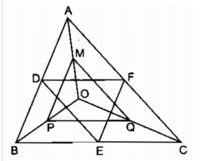
Theo giả thiết D, E, F lần lượt là trung điểm các cạnh AB, BC và CA nên DE, EF, FD là các đường trung bình của tam giác ABC. Do đó, ta có:
DE = 1/2 AC,EF = 1/2 AB,FD = 1/2 BC (1)
Mặt khác, M là trung điểm của OA, P là trung điểm của OB, Q là trung điểm của OC, xét các tam giác OAB, OBC, OCA, ta cũng có:
MP = 1/2 AB,PQ = 1/2 BC, QM = 1/2 AC. (2)
Từ đẳng thức (1) và (2), ta suy ra :
DE = QM, EF = MP, FD = PQ.
Do đó ta có: 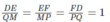
Vậy △ DEF đồng dạng △ QMP theo tỉ số đồng dạng k = 1, trong đó D, E, F lần lượt tương ứng với các đỉnh Q, M, P.
Đề thiếu số liệu của một góc nữa nên không thể sâp xếp
đề ko thiếu nha