3)tim x
a)(x-1).(y-2)=5
b)x.(y-3)=12
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 1:
A = 3(x + 1)2 + 5
Ta có: (x + 1)2 \(\ge\) 0 Với mọi x
\(\Rightarrow\) 3(x + 1)2 \(\ge\) 0 với mọi x
\(\Rightarrow\) 3(x + 1)2 + 5 \(\ge\) 5 với mọi x
Hay A \(\ge\) 5
Dấu "=" xảy ra khi và chỉ khi x + 1 = 5 hay x = -1
Vậy...
B = 2|x + y| + 3x2 - 10
Ta có: 2|x + y| \(\ge\) 0 với mọi x, y
3x2 \(\ge\) 0 với mọi x
\(\Rightarrow\) 2|x + y| + 3x2 - 10 \(\ge\) -10 với mọi x,y
Dấu "=" xảy ra khi và chỉ khi x + y = 0; x = 0
\(\Rightarrow\) x = y = 0
Vậy ...
C = 12(x - y)2 + x2 - 6
Ta có: 12(x - y)2 \(\ge\) 0 với mọi x; y
x2 \(\ge\) 0 với mọi x
\(\Rightarrow\) 12(x - y)2 + x2 - 6 \(\ge\) -6 với mọi x, y
Dấu "=" xảy ra khi và chỉ khi x = y = 0
Phần D ko rõ đầu bài nha vì D luôn có một giá trị duy nhất
Bài 2:
Phần A ko rõ đầu bài!
B = 3 - (x + 1)2 - 3(x + 2y)2
Ta có: -(x + 1)2 \(\le\) 0 với mọi x
-3(x + 2y)2 \(\le\) 0 với mọi x, y
\(\Rightarrow\) 3 - (x + 1)2 - 3(x + 2y)2 \(\le\) 3 với mọi x, y
Dấu "=" xảy ra khi và chỉ khi x = 2y; x + 1 = 0
\(\Rightarrow\) x = -1; y = \(\dfrac{-1}{2}\)
Vậy ...
C = -12 - 3|x + 1| - 2(y - 1)2
Ta có: -3|x + 1| \(\le\) 0 với mọi x
-2(y - 1)2 \(\le\) 0 với mọi y
\(\Rightarrow\) -12 - 3|x + 1| - 2(y - 1)2 \(\le\) -12 với mọi x, y
Dấu "=" xảy ra khi và chỉ khi x + 1 = 0; y - 1 = 0
\(\Rightarrow\) x = -1; y = 1
Vậy ...
Phần D đề ko rõ là \(\dfrac{5}{2x^2}-3\) hay \(\dfrac{5}{2}\)x2 - 3 nữa
F = \(\dfrac{-5}{3}\) - 2x2
Ta có: -2x2 \(\le\) 0 với mọi x
\(\Rightarrow\) \(\dfrac{-5}{3}-2x^2\) \(\le\) \(\dfrac{-5}{3}\) với mọi x
Dấu "=" xảy ra khi và chỉ khi x = 0
Vậy ...
Chúc bn học tốt!

a/ Ta có :
\(\left(x-1\right)\left(y-2\right)=5\)
Vì \(x,y\in N\Leftrightarrow x-1;y-2\in N\)\(,x-1;y-2\inƯ\left(5\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x-1=1\\y-2=5\end{matrix}\right.\\\left\{{}\begin{matrix}x-1=5\\y-2=1\end{matrix}\right.\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x=2\\y=7\end{matrix}\right.\\\left\{{}\begin{matrix}x=6\\y=3\end{matrix}\right.\end{matrix}\right.\)
Vậy ...........
b/ tương tự
a ) \(\left(x-1\right)\left(y-2\right)=5\)
Xảy ra 4 TH :
TH1 : \(\left[{}\begin{matrix}x-1=5\\y-2=1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=6\\y=3\end{matrix}\right.\)
TH2 : \(\left[{}\begin{matrix}x-1=-5\\y-2=-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-4\\y=1\end{matrix}\right.\)
TH3 : \(\left[{}\begin{matrix}x-1=1\\y-2=5\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\y=7\end{matrix}\right.\)
TH4 : \(\left[{}\begin{matrix}x-1=-1\\y-2=-5\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\y=-3\end{matrix}\right.\)
Vậy ........
b ) \(x\left(y-3\right)=12\)
Có 12TH xảy ra :
TH1 : \(\left[{}\begin{matrix}x=1\\y-3=12\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\y=15\end{matrix}\right.\)
TH2 : \(\left[{}\begin{matrix}x=-1\\y-3=-12\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-1\\y=-9\end{matrix}\right.\)
TH3 : \(\left[{}\begin{matrix}x=12\\y-3=1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=12\\y=4\end{matrix}\right.\)
TH4 : \(\left[{}\begin{matrix}x=-12\\y-3=-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-12\\y=2\end{matrix}\right.\)
TH5 : \(\left[{}\begin{matrix}x=2\\y-3=6\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\y=9\end{matrix}\right.\)
TH6 : \(\left[{}\begin{matrix}x=-2\\y-3=-6\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-2\\y=-3\end{matrix}\right.\)
TH7 : \(\left[{}\begin{matrix}x=6\\y-3=2\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=6\\y=5\end{matrix}\right.\)
TH8 : \(\left[{}\begin{matrix}x=-6\\y-3=-2\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-6\\y=1\end{matrix}\right.\)
TH9 : \(\left[{}\begin{matrix}x=3\\y-3=4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\\y=7\end{matrix}\right.\)
TH10 : \(\left[{}\begin{matrix}x=-3\\y-3=-4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-3\\y=-1\end{matrix}\right.\)
TH11 : \(\left[{}\begin{matrix}x=4\\y-3=3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=4\\y=6\end{matrix}\right.\)
TH12 : \(\left[{}\begin{matrix}x=-4\\y-3=-3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-4\\y=0\end{matrix}\right.\)
Vậy ....

Bài toán này có hai cách giải:
Cách 1: Thu gọn từng phương trình ta sẽ thu được phương trình bậc nhất hai ẩn x và y.
Cách 2: Đặt ẩn phụ.
Cách 1:
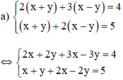
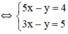 (hệ số của y bằng nhau nên ta trừ từng vế hai phương trình)
(hệ số của y bằng nhau nên ta trừ từng vế hai phương trình)
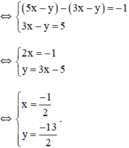
Vậy hệ phương trình có nghiệm duy nhất 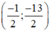
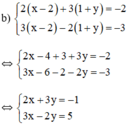
(Nhân hai vế pt 1 với 2; pt 2 với 3 để hệ số của y đối nhau)
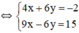 (Hệ số của y đối nhau nên ta cộng từng vế của hai pt)
(Hệ số của y đối nhau nên ta cộng từng vế của hai pt)
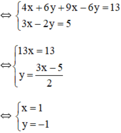
Vậy hệ phương trình có nghiệm duy nhất (1; -1).
Cách 2:
a) Đặt x + y = u và x – y = v (*)
Khi đó hệ phương trình trở thành
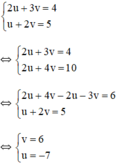
Thay u = -7 và v = 6 vào (*) ta được hệ phương trình:
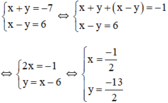
Vậy hệ phương trình có nghiệm 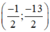
b) Đặt x – 2 = u và y + 1 = v.
Khi đó hệ phương trình trở thành :
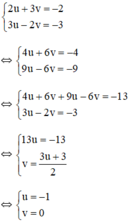
+ u = -1 ⇒ x – 2 = -1 ⇒ x = 1.
+ v = 0 ⇒ y + 1 = 0 ⇒ y = -1.
Vậy hệ phương trình có nghiệm (1; -1).

tim x,y,z biet 4/x+1=2/y-2=3/z+2 va xyz=12
\(\frac{4}{x+1}=\frac{2}{y-2}=\frac{3}{z+2}\)và \(xyz=12\)