g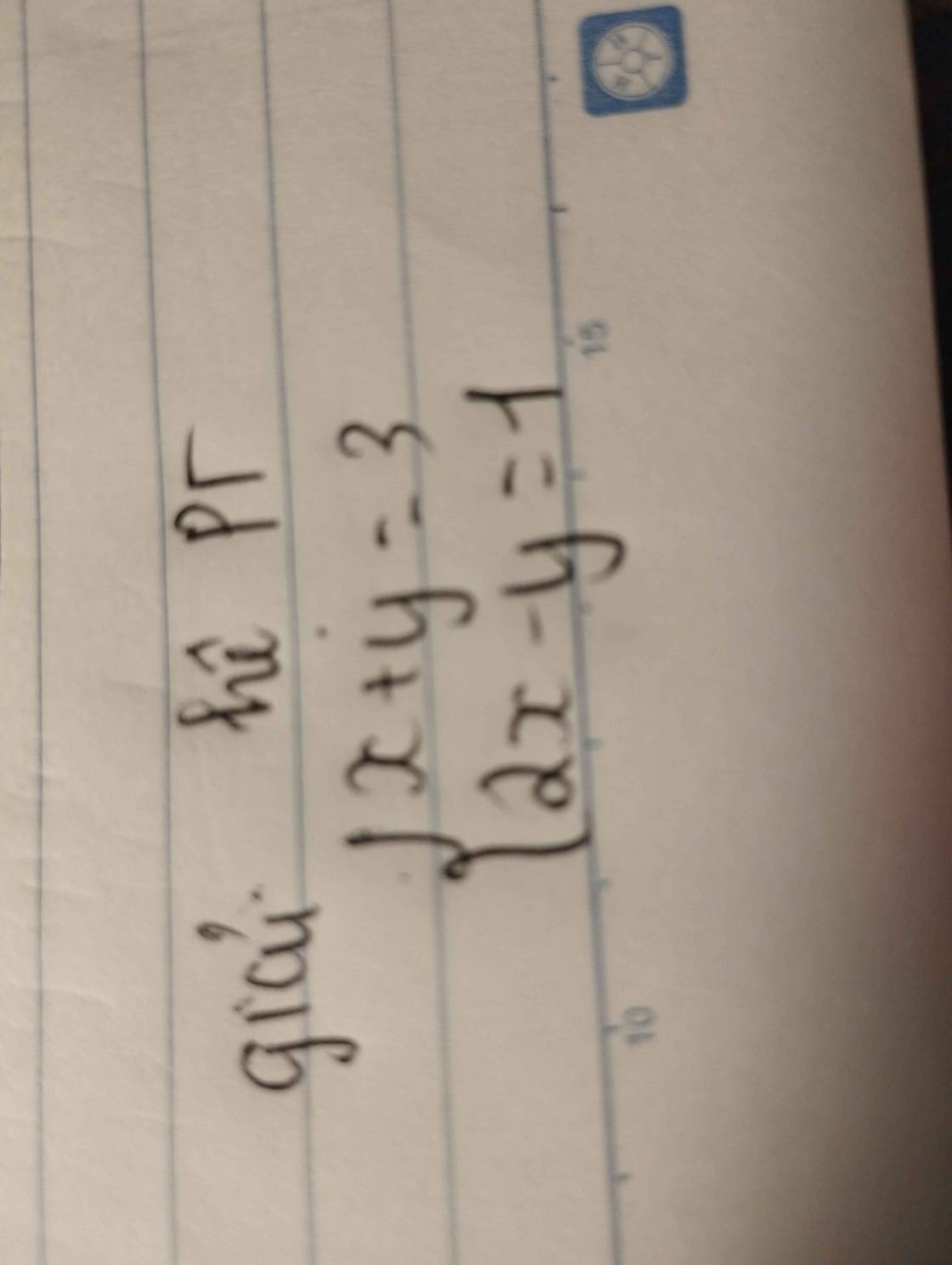 giải hệ phương trình
giải hệ phương trình
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\left\{{}\begin{matrix}A+G=50\%\\\dfrac{A}{G}=0,6\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}A+G=0,5\\\dfrac{A}{G}=0,6\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}A+G=0,5\\A=0,6G\end{matrix}\right.\)
Thay \(A=0,6G\) vào ta có:
\(\Leftrightarrow\left\{{}\begin{matrix}0,6G+G=0,5\\A=0,6G\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}1,6G=0,5\\A=0,6G\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}G=\dfrac{0,5}{1,6}\\A=0,6G\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}G=0,3125\\A=0,6\cdot0,3125\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}G=0,3125\\A=0,1875\end{matrix}\right.\)
Vậy: \(\left\{{}\begin{matrix}G=31,25\%\\A=18,75\%\end{matrix}\right.\)


Thay x = 3, y = 5 vào vế trái của phương trình (3) ta được:
VT = 5.3 – 2.5 = 15 – 10 = 5 = VP
Vậy (x; y) = (3; 5) là nghiệm của phương trình (3).
Hệ phương trình đã cho có nghiệm (x; ) = (3; 5)


Thay x = -3, y = 31/5 vào vế trái của phương trình (2), ta được:
VT = -3.(-3) + 2.31/5 = 9 + 62/5 = 107/5 ≠ 22 = VP
Vậy (x; y) = (-3; 31/5 ) không phải là nghiệm của phương trình (2).
Hệ phương trình đã cho vô nghiệm.

Mình mạn phép sửa lại phương trình $2$ của bạn là $mx+3y=1$ nhé.
ĐK: $m\neq 0$
a) Khi $m=2,$ hệ phương trình là:
\(\left\{{}\begin{matrix}-4x+y=5\\2x+3y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-4x+y=5\\4x+6y=2\end{matrix}\right.\Rightarrow7y=7\Leftrightarrow y=1\Rightarrow x=-1\)
b) \(\left\{{}\begin{matrix}-2mx+y=5\\mx+3y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-2mx+y=5\\2mx+6y=2\end{matrix}\right.\Rightarrow7y=7\Leftrightarrow y=1\Rightarrow x=-\dfrac{2}{m}\)
c) Do ta luôn có $y=1$ là số dương nên chỉ cần chọn $m$ sao cho:
\(x=-\dfrac{2}{m}>0\Leftrightarrow m< 0\)
d) \(x^2+y^2=1\Leftrightarrow\left(-\dfrac{2}{m}\right)^2+1^2=1\Leftrightarrow\dfrac{4}{m^2}=0\) (vô lý)
Vậy không tồn tại $m$ sao cho $x^2+y^2=1.$

a) Thay a=3 vào hệ pt, ta được:
\(\left\{{}\begin{matrix}4x-3y=6\\-5x+3y=8\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-x=14\\4x-3y=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-14\\-56-3y=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-14\\-3y=62\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=-14\\y=-\dfrac{62}{3}\end{matrix}\right.\)
Vậy: Khi a=3 thì hệ pt có nghiệm duy nhất là: \(\left(x,y\right)=\left(-14;-\dfrac{62}{3}\right)\)
tại sao cái bước chuyển đổi thứ 3 lại ra là {-56-3y=6 ạ

b: \(\left\{{}\begin{matrix}3x-2y=4\\2x+y=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x-2y=4\\4x+2y=10\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-x=-6\\2x+y=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=6\\y=5-2x=5-12=-7\end{matrix}\right.\)


 (1)
(1)
\(\left\{{}\begin{matrix}x+y=3\\2x-y=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x+y=3\\3x=4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{4}{3}+y=3\\x=\dfrac{4}{3}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=3-\dfrac{4}{3}\\x=\dfrac{4}{3}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{5}{3}\\x=\dfrac{4}{3}\end{matrix}\right.\)
Vậy: ...