viết phương trình chính tắc hypebol có tiêu điểm F(5; 0), cắt Oy tại C(0; 2)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Ta có \(2a = 20 \Rightarrow a = 10,2b = 16 \Rightarrow b = 8\).
Vậy phương trình chính tắc của elip có dạng \(\frac{{{x^2}}}{{100}} + \frac{{{y^2}}}{{64}} = 1\)
b) Ta có \(2a = 12 \Rightarrow a = 6,2c = 20 \Rightarrow c = 10\), suy ra \(b = \sqrt {{c^2} - {a^2}} = \sqrt {{{10}^2} - {6^2}} = 8\)
Vậy phương trình chính tắc của hypebol có dạng \(\frac{{{x^2}}}{{36}} - \frac{{{y^2}}}{{64}} = 1\)
c) Ta có tiêu điểm \(F\left( {\frac{1}{2};0} \right)\).
Do đó, \(\frac{p}{2} = \frac{1}{2}\) suy ra \(p = 1\).
Vậy phương trình chính tắc của parabol là \({y^2} = 2x\).

Ta có: \(2c = 10 \Rightarrow c = 5,2b = 6 \Rightarrow b = 3\)
Suy ra \(a = \sqrt {{c^2} - {b^2}} = \sqrt {{5^2} - {3^2}} = 4\)
Vậy phương trình chính tắc của hypebol có dạng \(\frac{{{x^2}}}{{16}} - \frac{{{y^2}}}{9} = 1\)

Chọn D.
Ta có: c = 2 a = 1 b 2 = c 2 - a 2 ⇒ a 2 = 1 b 2 = 3
Phương trình (H) : x 2 1 - y 2 3 = 1

a) Từ giả thiết ta có: \(a = 3,c = 5 \Rightarrow b = \sqrt {{c^2} - {a^2}} = \sqrt {{5^2} - {3^2}} = 4\)
Ta có phương trình chính tắc của hypebol là: \(\frac{{{x^2}}}{9} - \frac{{{y^2}}}{{16}} = 1\)
b) Ta có: \(2a = 8,2b = 6 \Rightarrow a = 4,b = 3\)
Suy ra phương trình chính tắc của hypebol là \(\frac{{{x^2}}}{{16}} - \frac{{{y^2}}}{9} = 1\)

Chọn B
Ta có a = 4 2 c = 10 b 2 = c 2 - a 2 ⇒ a = 4 c = 5 b = 3
Phương trình chính tắc của Hyperbol là
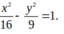

a) Nhập lệnh: Hypebon((-5,0),(5,0),(3,0)) vào ô nhập lệnh rồi bấm enter.
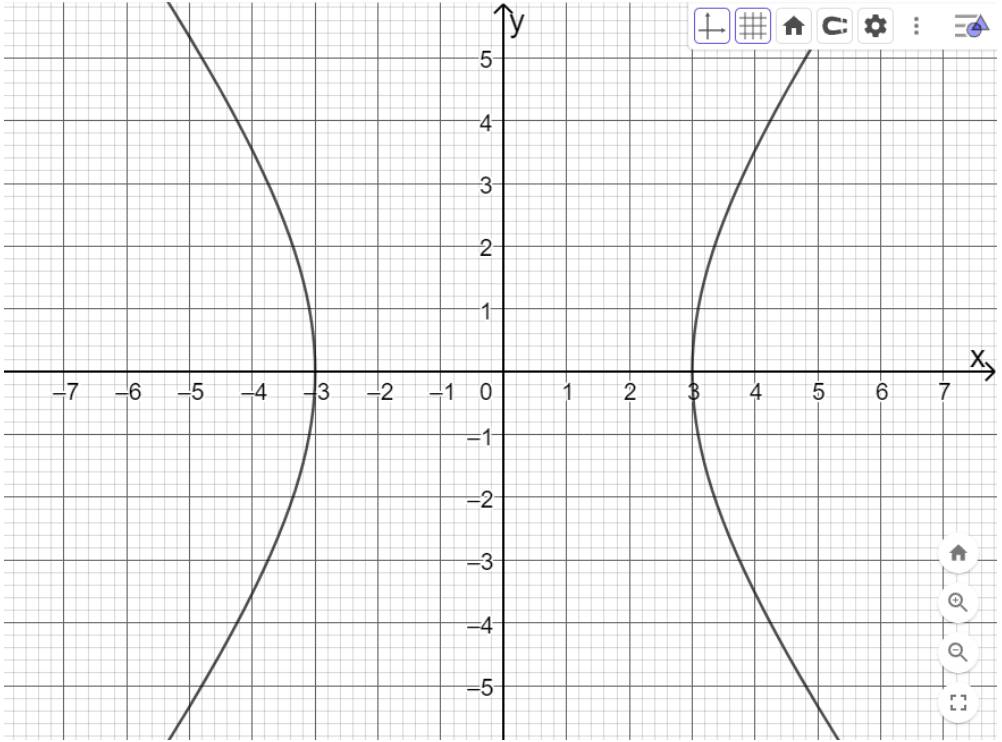
b) Nhập lệnh: y^2=5*x vào ô nhập lệnh rồi bấm enter
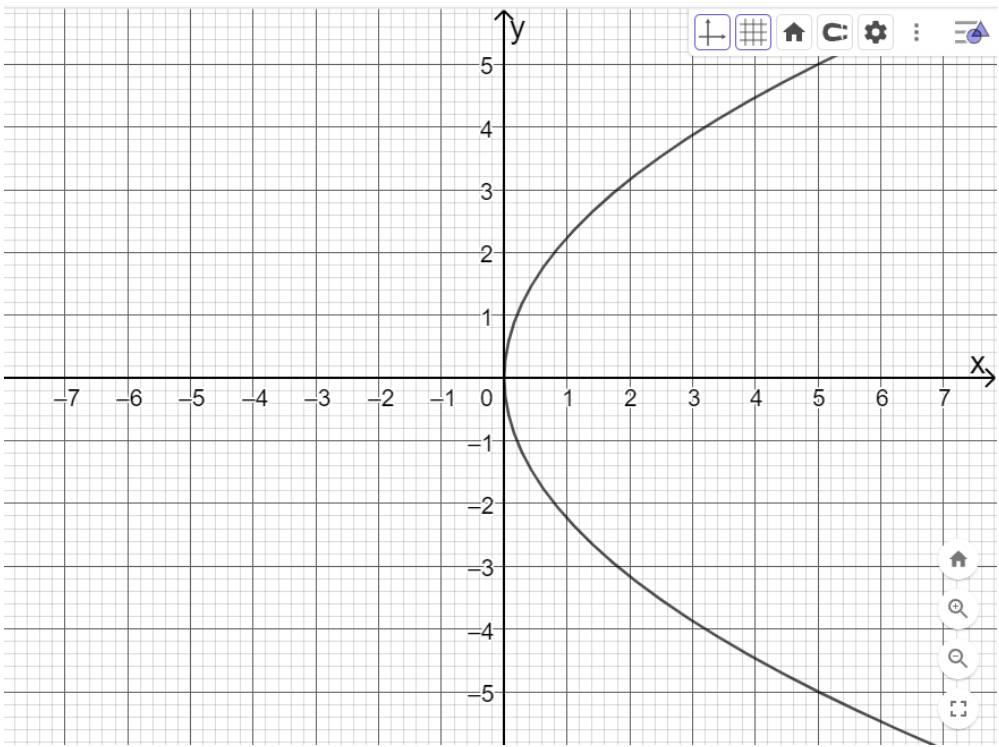
c)
Bước 1: Tạo thanh trượt a: Nháy vào biểu tượng thanh trượt, sau đó nháy cuột lên vùng làm việc, khi đó trên vùng làm việc xuất hiện bảng cho phép thiết lập thông tinh cho thanh trượt: Tên thanh trượt (a), giá trị dạng số/ số nguyên, giá trị cực tiểu (1), giá trị cực đại (10).
Bước 2: Tạo thanh trượt b: Làm tương tự với thiết lập thông tin chẳng hạn như:
Tên thanh trượt (b), giá trị dạng số, giá trị cực tiểu (0), giá trị cực đại (5), số gia (0,5).
Bước 3: Nhập phương trình chính tắc của elip vào ô Nhập lệnh:
x^2 / a^2 + y^2 / b^2 =1 và bấm enter.
Di chuyển trên thanh trượt vào giá trị a=3, b=1 ta được như hình dưới
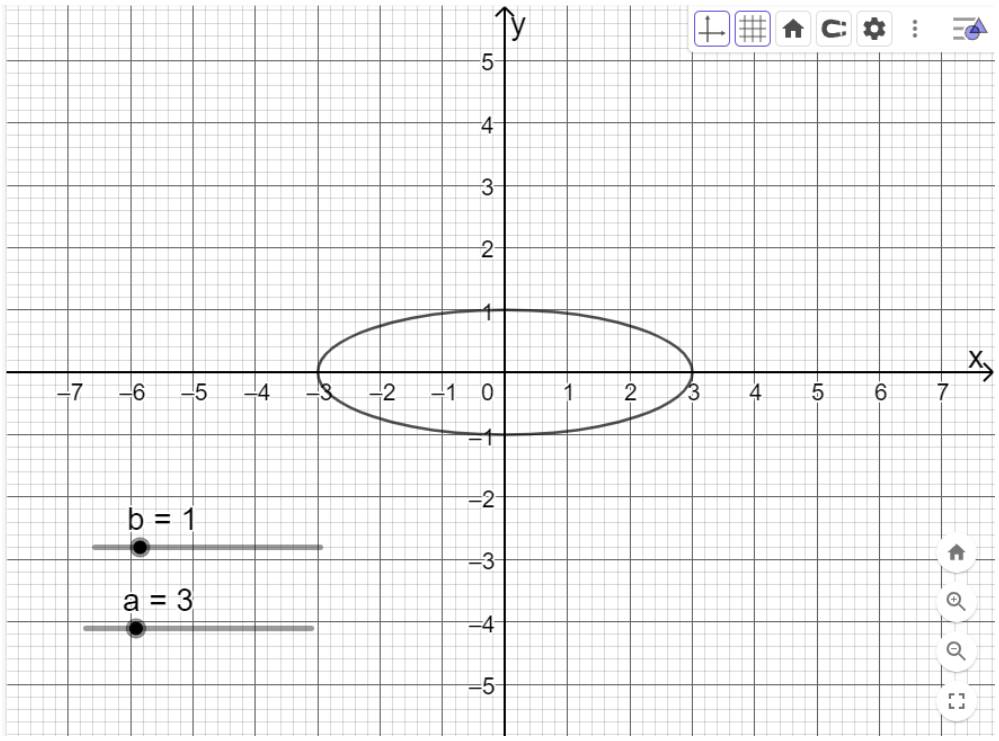
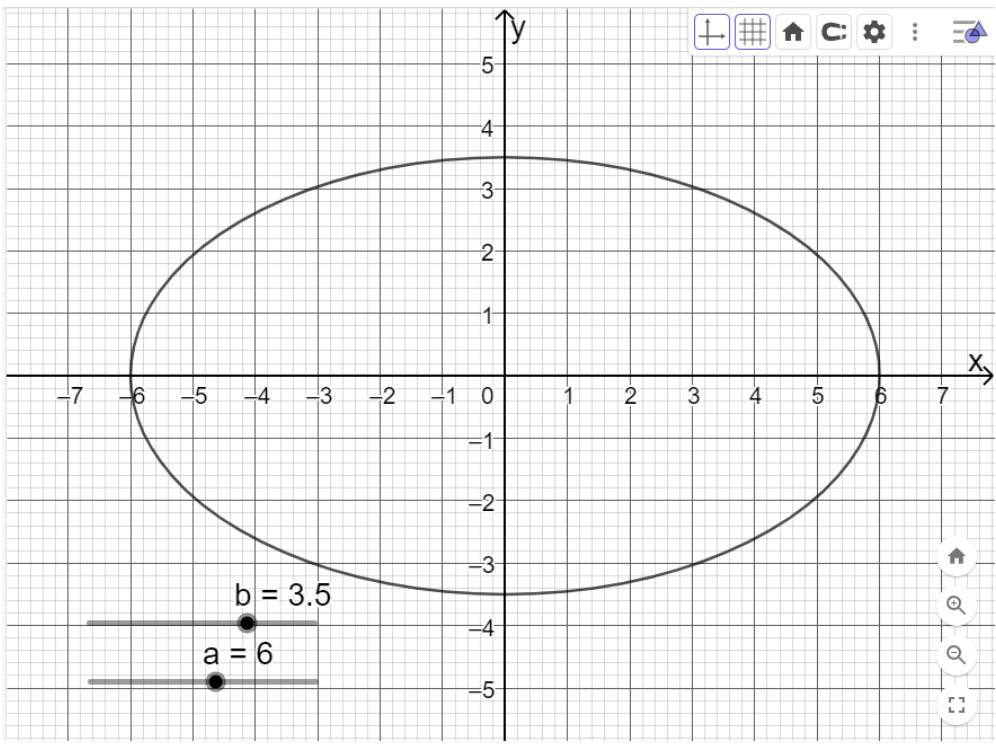
Di chuyển trên thanh trượt vào giá trị a=6, b=3,5 ta được như hình dưới

Do parabol có tiêu điểm là \(F\left( {6;0} \right)\) nên ta có \(\frac{p}{2} = 6 \Leftrightarrow p = 12\)
Vậy phương trình chính tắc của parabol là: \({y^2} = 24x\)


Ta có: F(5;0) nên \(\dfrac{p}{2}\)=5 ➝p=10
Vậy phương trình chính tắc của parabol (P): \(y^2\)= 2.10.x hay (P):\(y^2\)=20x
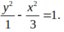
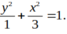
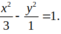
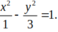
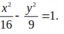
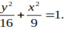
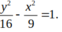
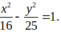
Tiêu điểm là F(5;0)
=>c=5
=>\(c^2=25\)
=>\(a^2+b^2=25\)
=>\(b^2=25-a^2\)
Phương trình chính tắc sẽ có dạng là \(\left(H\right):\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1\)
=>\(\dfrac{x^2}{a^2}-\dfrac{y^2}{25-a^2}=1\)
Thay x=0 và y=2 vào (H), ta được:
\(\dfrac{0^2}{a^2}-\dfrac{2^2}{25-a^2}=1\)
=>\(\dfrac{-4}{25-a^2}=1\)
=>\(25-a^2=-4\)
=>\(a^2=29\)
=>\(b^2=25-a^2=25-29=-4< 0\)
=>Không có phương trình chính tắc nào thỏa mãn yêu cầu đề bài