1, hai phân xưởng của một nhà máy theo kế hoạch phải làm tổng cộng 300 dụng cụ. nhưng khi thục hiện phân xưởng I vượt mức 10% kế hoạch của mình: phân xưởng II vượt mức 20% kế hoạch của mình, do đó cả hai phân xưởng đã làm đc 340 dụng cụ. tính số dụng cụ mỗi phân xưởng phải làm theo kế hoạch
2, một hình trụ cao 20cm. diện tích đáy bằng nửa diện tích xung quanh. trong chậu có nước cao đến 15cm . hỏi phải thêm bao nhiêu nước vào chậu để nước vừa đầy chậu

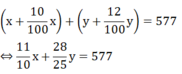
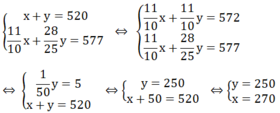
Bài 1:
Gọi số dụng cụ phân xưởng thứ nhất phải làm là a(dụng cụ)(Điều kiện: \(a\in Z^+\))
Số dụng cụ phân xưởng thứ hai phải làm là:
300-a(dụng cụ)
Theo đề, ta có:
\(\dfrac{11}{10}a+\dfrac{6}{5}\left(300-a\right)=340\)
\(\Leftrightarrow\dfrac{11}{10}a+360-\dfrac{6}{5}a=340\)
\(\Leftrightarrow\dfrac{-1}{10}a=-20\)
hay a=200(Thỏa ĐK)
Vậy: Phân xưởng thứ nhất phải làm 200 dụng cụ
Phân xưởng thứ hai phải làm 100 dụng cụ