Cho tam giác ABC . Trên nửa mặt phẳng bờ AC không chứa điểm B vẽ tia AD / góc CAD = góc ACB, trên nửa mặt phẳng bờ AB không chứa điểm C vẽ tia AE / góc EAB = góc ABC
Chứng tỏ 3 điểm E , A .D thẳng hàng
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
18 tháng 6 2018
Hình bạn tự vẽ được đúng không.
Ta có: góc DAC = góc ACB (gt)
Mà hai góc này ở vị trí so le trong đối với hai đường thẳng DA, BC và cát tuyến AC.
=> AD//BC (dhnb 2 đường thẳng //) (1)
CM tương tự với góc EAB, ABC
=> EA//BC (2)
Từ (1) và (2) => AD//EA
=> E,A,D thẳng hàng.
18 tháng 6 2018
Ta có: góc DAC = góc ACB (gt)
Mà hai góc này ở vị trí so le trong đối với hai đường thẳng DA, BC và cát tuyến AC.
=> AD//BC (dhnb 2 đường thẳng //) (1)
CM tương tự với góc EAB, ABC
=> EA//BC (2)
Từ (1) và (2) => AD//EA
=> E,A,D thẳng hàng.
12 tháng 9 2017
Mik vẽ hình thấy sai thì phải. Góc ACB , không phải góc ABC
CM
31 tháng 3 2018
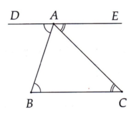
a) Có B A D ^ = A B C ^ ( giả thiết),
Mà hai góc ở vị trí so le trong nên AD // BC (theo tính chất hai đường thẳng song song).
b) Tương tự ý a), chứng minh được AE // BC
Theo tiên đề ơ-clit, hai đường thẳng AE và AD trùng nhau. Từ đó ba điểmD, A, E thẳng hàng.