giúp hộ mình bài này
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Mình làm với ví dụ khác được không? Mình nghĩ ko nên làm đúng bài ý tại vì nên xem một ví dụ khác rồi vận dụng làm theo hiệu quả hơn ý. Được ko bạn?

e: \(=\dfrac{-3}{4}+\dfrac{5}{7}=\dfrac{-21+20}{28}=\dfrac{-1}{28}\)
a ) \(\dfrac{6}{13}\) + \(\dfrac{-14}{39}\)
= \(\dfrac{6.3}{13.3}\) + \(\dfrac{-14}{39}\)
= \(\dfrac{18}{39}\) - \(\dfrac{14}{39}\)
= \(\dfrac{4}{39}\)
{ các ý còn lại tương tự }


a) nCuCl2 = 0,15.2 = 0,3 (mol)
PTHH: 2Al + 3CuCl2 --> 2AlCl3 + 3Cu
____0,2<------0,3--------->0,2---->0,3
=> m = 0,3.64 - 0,2.27 = 13,8 (g)
b) \(C_{M\left(AlCl_3\right)}=\dfrac{0,2}{0,15}=1,3333M\)

Bài 4:
\(a,A=\dfrac{x-1}{\sqrt{x}\left(\sqrt{x}-1\right)}=\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\sqrt{x}\left(\sqrt{x}-1\right)}=\dfrac{\sqrt{x}+1}{\sqrt{x}}\\ P=A:B=\dfrac{\sqrt{x}+1}{\sqrt{x}}\cdot\dfrac{x-1}{\sqrt{x}+1}=\dfrac{x-1}{\sqrt{x}}\\ b,P\sqrt{x}=m-\sqrt{x}+x\\ \Leftrightarrow x-1=m-\sqrt{x}+x\\ \Leftrightarrow m=\sqrt{x}-1\)

Bài văn có ba phần:
+ Mở bài (câu văn đầu): Nhận xét chung về nắng trưa.
+ Thân bài: Tả cảnh vật trong nắng trưa, gồm các đoạn nhỏ:
- Đoạn 1 (Từ Buổi trưa ngồi trong nhà... đến ...bốc lên mãi): Hơi đất trong nắng trưa gay gắt.
- Đoạn 2 (Từ Tiếng gì xa vắng... đến ...hai mi mắt khép lại): Tiếng võng đưa và câu hát ru rời rạc trong nắng trưa.
- Đoạn 3 (Từ Con gà nào... đến ...bóng duối cũng lặng im): Cây cối và con vật trong nắng trưa.
- Đoạn 4 (Từ Ấy thế mà... đến ...cấy nốt thửa ruộng chưa xong): Hình ảnh người mẹ làm việc vất vả trong nắng trưa.
+ Kết bài (câu cuối - Kết bài mở rộng):
Cảm nghĩ về mẹ: Thương mẹ biết bao nhiêu, mẹ ơi!

(x + 2)(x + 5) < 0
Th1: x + 2 > 0 => x > -2
x + 5 < 0 => x < -5
=> Vô lý
Th2: x + 2 < 0 => x < -2
x + 5 > 0 => x > -5
=> -5 < x < -2
Ta có : (x+2)(x+5)<0
=> x+2 và x+5 là hai số nguyên trái dấu
mà x+5 > x+2
=> \(\hept{\begin{cases}x+5>0\\x+2< 0\end{cases}}\)
=> \(\hept{\begin{cases}x>-5\\x< 2\end{cases}}\)
=> \(-5< x< 2\)
=> \(x\in\left\{-4;-3;-2;-1;0;1\right\}\)
~ học tốt nha ~

Bài 5 hình 1: (tự vẽ hình nhé bạn)
a) Xét ΔABD và ΔACB ta có:
\(\widehat{BAD}\)= \(\widehat{BAC}\) (góc chung)
\(\widehat{ABD}\)= \(\widehat{ACB}\) (gt)
=> ΔABD ~ ΔACB (g-g)
=> \(\dfrac{AB}{AC}\) = \(\dfrac{BD}{CB}\) = \(\dfrac{AD}{AB}\) (tsđd)
b) Ta có: \(\dfrac{AB}{AC}\) = \(\dfrac{AD}{AB}\) (cm a)
=> \(AB^2\) = AD.AC
=> \(2^2\) = AD.4
=> AD = 1 (cm)
Ta có: AC = AD + DC (D thuộc AC)
=> 4 = 1 + DC
=> DC = 3 (cm)
c) Xét ΔABH và ΔADE ta có:
\(\widehat{AHB}\) = \(\widehat{AED}\) (=\(90^0\))
\(\widehat{ADB}\) = \(\widehat{ABH}\) (ΔABD ~ ΔACB)
=> ΔABH ~ ΔADE
=> \(\dfrac{AB}{AD}\) = \(\dfrac{AH}{AE}\) = \(\dfrac{BH}{DE}\) (tsdd)
Ta có: \(\dfrac{S_{ABH}}{S_{ADE}}\) = \(\left(\dfrac{AB}{AD}\right)^2\)= \(\left(\dfrac{2}{1}\right)^2\)= 4
=> đpcm
Tiếp bài 5 hình 2 (tự vẽ hình)
a) Xét ΔABC vuông tại A ta có:
\(BC^2\) = \(AB^2\) + \(AC^2\)
\(BC^2\) = \(21^2\) + \(28^2\)
BC = 35 (cm)
b) Xét ΔABC và ΔHBA ta có:
\(\widehat{BAC}\) = \(\widehat{AHB}\) ( =\(90^0\))
\(\widehat{ABC}\) = \(\widehat{ABH}\) (góc chung)
=> ΔABC ~ ΔHBA (g-g)
=> \(\dfrac{AB}{BH}\) = \(\dfrac{BC}{AB}\) (tsdd)
=> \(AB^2\) = BH.BC
=> \(21^2\) = 35.BH
=> BH = 12,6 (cm)
c) Xét ΔABC ta có:
BD là đường p/g (gt)
=> \(\dfrac{AD}{DC}\) = \(\dfrac{AB}{BC}\) (t/c đường p/g)
Xét ΔABH ta có:
BE là đường p/g (gt)
=> \(\dfrac{HE}{AE}\) = \(\dfrac{BH}{AB}\) (t/c đường p/g)
Mà: \(\dfrac{AB}{BC}\) = \(\dfrac{BH}{AB}\) (cm b)
=> đpcm
d) Ta có: \(\left\{{}\begin{matrix}\widehat{HBE}+\widehat{BEH}=90^0\\\widehat{ABD}+\widehat{ADB=90^0}\\\widehat{HBE}=\widehat{ABD}\end{matrix}\right.\)
=> \(\widehat{BEH}=\widehat{ADB}\)
Mà \(\widehat{BEH}=\widehat{AED}\) (2 góc dd)
Nên \(\widehat{ADB}=\widehat{AED}\)
=> đpcm

đề như thế này à \(\dfrac{\sqrt{27-3\sqrt{2}+2\sqrt{6}}}{3\sqrt{3}}\)
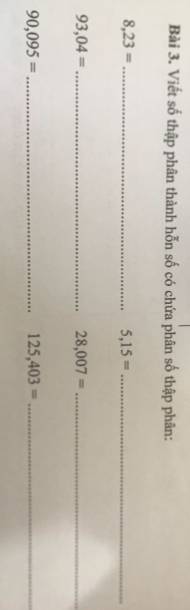

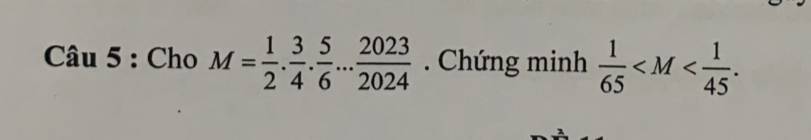


 giải hộ mình mấy bài này vs ạ !
giải hộ mình mấy bài này vs ạ !
a:Có 10 tam giác
Các tam giác trong hình là: ΔADE, ΔDGE, ΔEGC, ΔDGB; ΔGBC; ΔDBC; ΔDEC; ΔEBC; ΔDBE; ΔABC
b: Xét ΔABC có \(\dfrac{AD}{AB}=\dfrac{AE}{AC}\)
nên DE//BC
Xét ΔABC có DE//BC
nên \(\dfrac{DE}{BC}=\dfrac{AD}{AB}=\dfrac{1}{3}\)
Vì DE//BC
nên \(\dfrac{DG}{CG}=\dfrac{EG}{GB}=\dfrac{DE}{BC}=\dfrac{1}{3}\)
Vì EG/GB=1/3 nên \(S_{DGE}=\dfrac{1}{3}\cdot S_{DGB}\)
=>\(S_{DGB}=3\cdot S_{DEG}\)
Vì DG/CG=1/3 nên \(S_{DGE}=\dfrac{1}{3}\cdot S_{CGE}\)
=>\(S_{CGE}=3\cdot S_{DGE}\)
=>\(S_{DGB}=S_{CGE}\)