cho biểu thức : M = x2+y2+2z2+t2
với x,y,z là các số nguyên không âm . tìm giá triij nhỏ nhất của M và các giá trị tương ứng của x,y,z và t biết rằng :
x2-y2+t2=21
x2+3y2+4z2=101
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
a. Vì $x,y$ tỉ lệ nghịch nên đặt $xy=k$ với $k$ là số thực nào đó.
Ta có:
$x_1y_1=k=x_2y_2$
$\Leftrightarrow 7x_1=8y_2\Rightarrow x_1=\frac{8}{7}y_2$
Thay vô điều kiện 1 thì:
$2.\frac{8}{7}y_2-3y_2=30$
$\Leftrightarrow y_2=-42$
$x_1=\frac{8}{7}y_2=-48$
b. Từ kết quả phần a suy ra:
$xy=x_1y_1=-48.7=-336$
$\Rightarrow y=\frac{-336}{x}$

\(A\le\sqrt{3\left(x+y+y+z+z+x\right)}=\sqrt{6\left(x+y+z\right)}\le\sqrt{6.\sqrt{3\left(x^2+y^2+z^2\right)}}=\sqrt{6\sqrt{3}}\)
\(A_{max}=\sqrt{6\sqrt{3}}\) khi \(x=y=z=\dfrac{1}{\sqrt{3}}\)
Do \(x^2+y^2+z^2=1\Rightarrow0\le x;y;z\le1\)
\(\Rightarrow\left\{{}\begin{matrix}x^2\le x\\y^2\le y\\z^2\le z\end{matrix}\right.\) \(\Rightarrow x+y+z\ge x^2+y^2+z^2=1\)
\(A^2=2\left(x+y+z\right)+2\sqrt{\left(x+y\right)\left(x+z\right)}+2\sqrt{\left(x+y\right)\left(y+z\right)}+2\sqrt{\left(y+z\right)\left(z+x\right)}\)
\(A^2=2\left(x+y+z\right)+2\sqrt{x^2+xy+yz+zx}+2\sqrt{y^2+xy+yz+zx}+2\sqrt{z^2+xy+yz+zx}\)
\(A^2\ge2\left(x+y+z\right)+2\sqrt{x^2}+2\sqrt{y^2}+2\sqrt{z^2}=4\left(x+y+z\right)\ge4\)
\(\Rightarrow A\ge2\)
\(A_{min}=2\) khi \(\left(x;y;z\right)=\left(0;0;1\right)\) và các hoán vị

x và y tỉ lệ nghịch
=>x1y1=x2y2
=>y1/x2=y2/x1
=>y1/5,6=y2/3,4=(5y1-3y2)/(5*5,6-3*3,4)=35,6/17,8=2
=>y1=11,2; y2=6,8

Chọn đáp án B
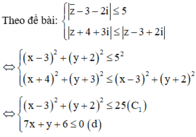
=> Tập hợp các điểm biểu diễn số phức z là miền mặt phẳng (T) mà tọa độ các điểm thỏa mãn hệ (*)
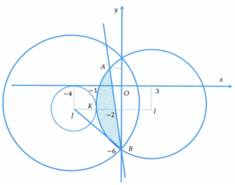
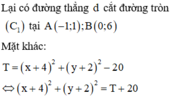


Chọn đáp án B

Từ giả thiết ta có:
![]()
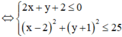
Suy ra tập hợp các điểm biểu diễn số phức z là miền mặt phẳng
(T) thỏa mãn 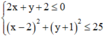 (miền tô đậm trong hình vẽ bên
(miền tô đậm trong hình vẽ bên
Gọi A, B là các giao điểm của đường thẳng 2 x + y + 2 = 0 và đường tròn (C’) : x - 2 2 + y + 1 2 = 25
Ta tìm được A(2; -6) và B(-2; 2)
Ta có :
![]()
![]()
Đường tròn (C) cắt miền (T) khi và chỉ khi
![]()
![]()
![]()

Với x và y là hai đại lượng tỉ lệ nghịch nên x 1 y 1 = x 2 y 2 mà x 2 = − 3 ; y 1 = 8 và 4 x 1 + 3 y 2 = 24

\(\hept{\begin{cases}x^2-y^2+t^2=21\left(1\right)\\x^2+3y^2+4z^2=101\left(2\right)\end{cases}}\)
Cộng (1) và (2) ta có :
\(2x^2+2y^2+4z^2+t^2=122\Leftrightarrow2\left(x^2+y^2+2z^2+t^2\right)-t^2=122\)
\(\Rightarrow2M=122+t^2\ge122\Rightarrow m\ge61\Rightarrow Min_M=61.\)
Khi \(t=0\Rightarrow\hept{\begin{cases}x^2-y^2=21\\x^2+3y^2+4z^2=101\left(3\right)\end{cases}.}\)
Vì x, y nguyên không âm nên :
\(\left(x-y\right)\left(x+y\right)=21\)
TH1: \(\hept{\begin{cases}x-y=1\\x+y=21\end{cases}\Leftrightarrow}\hept{\begin{cases}x=11\\y=10\end{cases}}\)Thế vào (3) ta được \(4z^2=-320\left(loại\right).\)
TH2: \(\hept{\begin{cases}x-y=3\\x+y=7\end{cases}\Leftrightarrow}\hept{\begin{cases}x=5\\y=2\end{cases}.}\)Thế vào (3) ta được \(4z^2=64\Leftrightarrow z^2=16\Leftrightarrow z=4\left(z\ge0\right).\)
Vậy ta tìm được \(\left(x,y,z,t\right)=\left(5;2;4;0\right)\)thì \(Min_M=61.\)
cộng vế 2 cái đẳng thức đề cho, đc: \(2x^2+2y^2=122-t^2-4z^2\) \(\Rightarrow x^2+y^2=61-\frac{t^2}{2}-2z^2\)
Thay vào M đc: \(M=61+\frac{t^2}{2}\) (t nguyên ko âm) => Min M = 61 khi t =0
Giải hệ \(\hept{\begin{cases}x^2+3y^2+4z^2=101\\x^2+y^2+2z^2=61\\x^2-y^2=21\end{cases}}\)sẽ ra đc giá trị của x2, y2, z2. nhưng hệ này vô số nghiệm thì phải