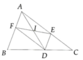
cho tg ABC, D là 1 điểm trên cạnh BC. Qua D kẻ đg thẳng song song với AB cắt AC ở E. Trên cạnh AB lấy F sao cho AF=DE. Gọi I là trung điểm của AD. Cmr:
a) DF=AE
b) E và F đối xứng nhau qua I
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CH
Cô Hoàng Huyền
Admin
VIP
15 tháng 10 2018
Con tham khảo tại link dươi đây nhé:
Câu hỏi của Trần Thị Vân Ngọc - Toán lớp 8 - Học toán với OnlineMath
CH
Cô Hoàng Huyền
Admin
VIP
15 tháng 10 2018
.png)
a) Xét tứ giác AEDF có DE song song và bằng AF nên AEDF là hình bình hành (Dấu hiệu nhận biết).
Vậy thì AE = FD (tính chất hình bình hành)
b) Do AEDF là hình bình hành nên hai đường chéo AD và EF cắt nhau tại trung điểm mỗi đường.
Theo đề bài thì I là trung điểm AD nên I cũng là trung điểm EF.
Vậy E đối xứng với F qua I.
30 tháng 5 2017
a)Xét tam giác DAF và tam giác ADE , ta có
AF=DE(gt)
góc DAF=góc ADE ( 2 góc so le trong của AB song song DE)
AD là cạnh chung
=>tam giác DAF=tam giác ADE(c.g.c)
=>DF=AE(2 cạnh tương ứng)
b)Xét tứ giác AFDE có:
AF=DE(gt)
AF song song DE
=> tứ giác AFDE là hình bình hành (tứ giác có cặp cạnh đối vừa bằng nhau vừa song song)
mà I là trung điểm của đường chéo AD (gt)
=> I cũng là trung điểm của đường chéo EF
=> E và F đối xứng với nhau qua điểm I
CH
Cô Hoàng Huyền
Admin
VIP
15 tháng 10 2018
Con tham khảo tại link dươi đây nhé:
Câu hỏi của Trần Thị Vân Ngọc - Toán lớp 8 - Học toán với OnlineMath
CM
19 tháng 4 2017
Ta chứng minh được AEDF là hình bình hành Þ AD Ç È = I. I là trung điểm của AD và EF. Suy ra E đối xứng với F qua I
Con tham khảo tại link dươi đây nhé:
Câu hỏi của Trần Thị Vân Ngọc - Toán lớp 8 - Học toán với OnlineMath
Trả lời:
-Bạn tham khảo link dưới đây nhé!
https://olm.vn/hoi-dap/detail/194103532337.html
#Trúc Mai