Giải phương trình : [(3 căn x+6/x-4) + (căn x/căn x -2)] : (x-9/căn x-3)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) \(6\sqrt{x-1}-\dfrac{1}{3}\cdot\sqrt{9x-9}+\dfrac{7}{2}\sqrt{4x-4}=24\) (ĐK: \(x\ge1\))
\(\Leftrightarrow6\sqrt{x-1}-\dfrac{1}{3}\cdot\sqrt{9\left(x-1\right)}+\dfrac{7}{2}\sqrt{4\left(x-1\right)}=24\)
\(\Leftrightarrow6\sqrt{x-1}-\dfrac{1}{3}\cdot3\sqrt{x-1}+\dfrac{7}{2}\cdot2\sqrt{x-1}=24\)
\(\Leftrightarrow6\sqrt{x-1}-\sqrt{x-1}+7\sqrt{x-1}=24\)
\(\Leftrightarrow12\sqrt{x-1}=24\)
\(\Leftrightarrow\sqrt{x-1}=\dfrac{24}{12}\)
\(\Leftrightarrow\sqrt{x-1}=2\)
\(\Leftrightarrow x-1=4\)
\(\Leftrightarrow x=4+1\)
\(\Leftrightarrow x=5\left(tm\right)\)
b) \(\dfrac{1}{2}\sqrt{4x+8}-2\sqrt{x+2}-\dfrac{3}{7}\sqrt{49x+98}=-8\) (ĐK: \(x\ge-2\))
\(\Leftrightarrow\dfrac{1}{2}\cdot2\sqrt{x+2}-2\sqrt{x+2}-\dfrac{3}{7}\cdot7\sqrt{x+2}=-8\)
\(\Leftrightarrow\sqrt{x+2}-2\sqrt{x+2}-3\sqrt{x+2}=-8\)
\(\Leftrightarrow-4\sqrt{x+2}=-8\)
\(\Leftrightarrow\sqrt{x+2}=\dfrac{-8}{-4}\)
\(\Leftrightarrow\sqrt{x+2}=2\)
\(\Leftrightarrow x+2=4\)
\(\Leftrightarrow x=4-2\)
\(\Leftrightarrow x=2\left(tm\right)\)

√(2x²+8x+6) + √(x²-1) = 2(x+1) TXĐ: x € (-∞;-3] U [1;+∞) U {-1}
Từ pt => x≥ -1. Kết hợp với TXĐ đc: x ≥1 hoặc x = -1
Bình phương 2 vế:
2√[2(x²-1)(x²+4x+3)] = x²-1
Từ đây suy ra x² ≥ 1, lại bình phương 2 vế tiếp:
8(x²-1)(x²+4x+3) = x^4 - 2x²+1
<=> 7x^4 + 32x³ + 18x² -32x -25 = 0
<=> 7x^4 - 7x² + 32x³ - 32x +25x² - 25 = 0
<=> 7x²(x²-1) + 32x(x²-1) +25(x²-1) = 0
<=> (x²-1)(7x²+32x+25) = 0
<=> (x²-1)(x+1)(7x+25) = 0
<=> x = ±1 (x = -25/7 loại)
hình như bạn hiểu sai đề rồi. viết lại cho rõ nhé:(8x-6)căn (x-1)=(2+căn (x-2))(x+4 căn(x-2)+3)


1 ) đặt ẩn phụ
căn(x+4) = a
căn(4-x) = b
=> a^2 + b^2 = 8 ; a^2 - b^2 = 2x
Thay vào phương trình giải rất dễ
2) điều kiện xác định " x lớn hơn hoặc = 1
từ ĐKXĐ => vế trái lớn hơn hoặc = 1
=> 2 - x lớn hơn hoặc = 1
=> x nhỏ hơn hoặc = 1
kết hợp ĐKXĐ => x = 1
3) mk chưa biết làm

Câu 1:
Dễ thấy phương trình có x=2 là 1 nghiệm.
Mặt khác ta có: vế trái luôn nghịch biến do
Vậy phương trình có nghiệm duy nhất x=2
Câu 2:
Áp dụng bất đẳng thức Côsi ta có:
Dễ thấy chỉ xảy ra khi
Mặt khác khi thay x=2 vào vế trái được VT bằng
Vậy kết luận phương trình đã cho vô nghiệm.
Câu 3:
Tương tự phương pháp như câu 2 ta có:
Vế phải
mà
Vậy nên chỉ có thể xảy ra khi
Mặt khác ta có để
Thay x=0 vào (1) được (Thoả mãn)
Vậy phương trình đã cho có nghiệm x=0
Câu 4
Điều kiện là mẫu khác 0 hay x khác
Với điều kiện trên ta có:%20%5CLeftrightarrow%20(2%5E%7Bx%7D)%5E%7B3%7D-5(2%5E%7Bx%7D)%5E%7B2%7D+2%5E%7Bx%7D+10=0)
Bạn đặtta được phương trình sau
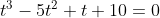
Giải phương trình được,
(loại vì t>0)
Vậy cuối cùng giải ra nghiệm của phương trình là:và

Bạn nên viết đề bằng công thức toán để được hỗ trợ tốt hơn (biểu tượng $\sum$ góc trái khung soạn thảo). Viết thế này khó dịch quá.