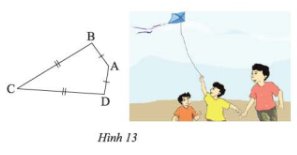
tứ giác ABCD có \(\widehat{B}\)+ \(\widehat{D}\)+ 180O và CB = CD. chứng minh AC là tia phân giác của \(\widehat{A}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
14 tháng 5 2017
ta có : \(\widehat{A}+\widehat{B}=180\)=> AD // BC ( 2 góc trong cùng phía có tổng 180) => ABCD là hình thang
mặt khác: CB=CD => ABCD là hình bình hành ( hình thang có 2 cạnh kề bằng nhau là hình bình hành)
Dễ thấy AC là đường chéo của ABCD => AC là tia phân giác của \(\widehat{A}\)(đường chéo của hình bình hành là tia pg của 2 đỉnh )
HQ
Hà Quang Minh
Giáo viên
8 tháng 9 2023
a) Ta có:
\(AB = AD\) (gt) nên \(A\) thuộc đường trung trực của \(BD\)
\(CB = CD\) (gt) nên \(C\) thuộc đường trung trực của \(BD\)
Vậy \(AC\) là đường trung trực của \(BD\)
b) Xét \(\Delta ABC\) và \(\Delta ADC\) ta có:
\(AB = AD\) (gt)
\(BC = CD\) (gt)
\(AC\) chung
Suy ra: \(\Delta ABC = \Delta ADC\) (c-g-c)
Suy ra: \(\widehat {ABC} = \widehat {ADC} = 95^\circ \) (hai góc tương ứng)
Trong tứ giác \(ABCD\), tổng các góc bằng \(360^\circ \) nên:
\(\widehat A = 360^\circ - \left( {95^\circ + 35^\circ + 95^\circ } \right) = 135^\circ \)
15 tháng 7 2023
a) Ta có : AB=BC và CD=DA (đề bài)
⇒ BD là đường trung trực của AC
b) Ta có : AB=BC (đề bài)
⇒ Δ ABC cân tại B
⇒ Góc BAC = Góc BCA
Tương tự ta chứng minh Góc DAC = Góc DCA (CD=AD...)
mà Góc A = Góc BAC + Góc DAC
Góc C = Góc BCA+ Góc DCA
⇒ Góc A = Góc C
mà A + B + C +D =360; B=100o ; D=80o
⇒ A + C =360 - (100 + 80) = 240
⇒ A = C = 240 : 2 = 120o