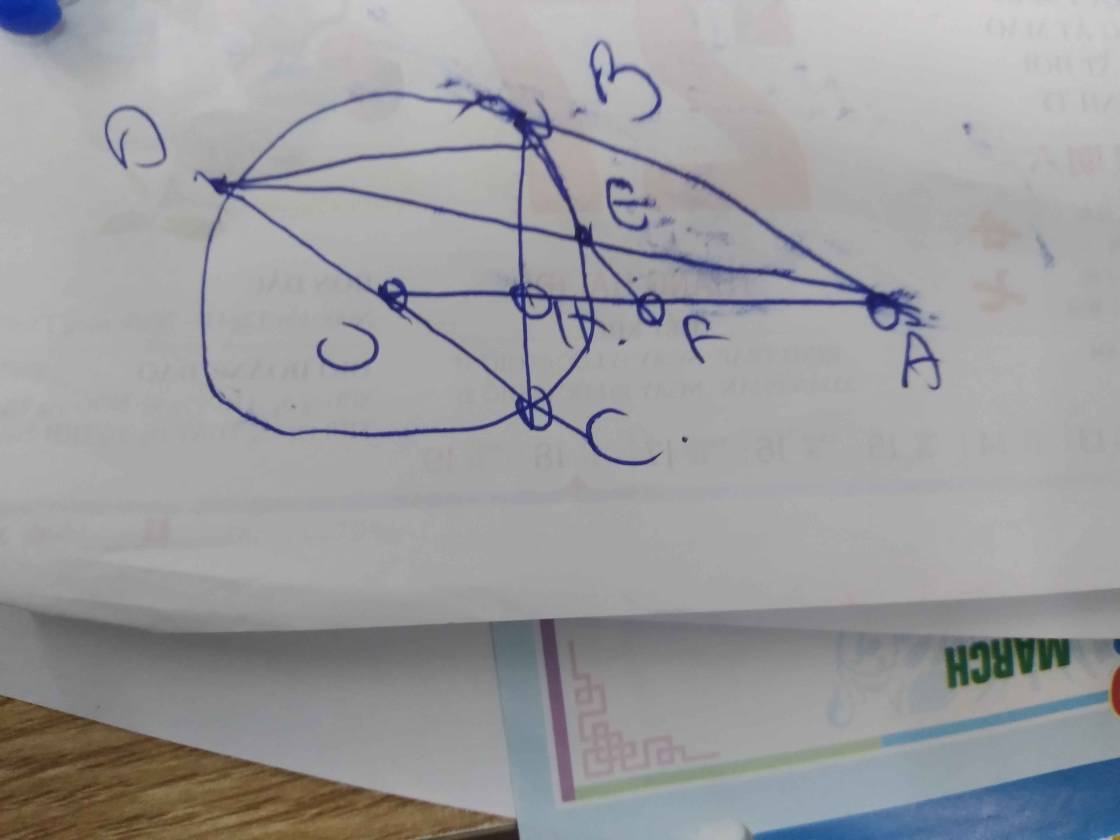
Từ 1 điểm A nằm ngoài đt (O;R)kẻ các tiếp tuyến AB,AC,BC vc đt (B,C là các tiếp điểm). Trên cung nhỏ BC lấy 1 điểm M bất khác B và C.Gọi I,K,P lần lượt là hình chiếu vuong góc của điêm M tên các đoạn thẳng AB,AC,BC.
1.CM tứ giác AIMK nội tiếp
2.CM góc MPK=MBC