16 x 17 x 18 x ...... x 2016 x 2017
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\frac{x+18}{2018}+\frac{x+17}{2017}+\frac{x+16}{2016}=3\)
\(\Rightarrow\frac{x+18}{2018}-1+\frac{x+17}{2017}-1+\frac{x+16}{2016}-1=3-3\)
\(\Rightarrow\frac{x+18-2018}{2018}+\frac{x+17-2017}{2017}+\frac{x+16-2016}{2016}=0\)
\(\Rightarrow\frac{x-2000}{2018}+\frac{x-2000}{2017}+\frac{x-2000}{2016}=0\)
\(\Rightarrow\left(x-2000\right)\left(\frac{1}{2018}+\frac{1}{2017}+\frac{1}{2016}\right)=0\)
Vì \(\frac{1}{2018}+\frac{1}{2017}+\frac{1}{2016}\ne0\)
=> x - 2000 = 0
=> x = 2000
Ta có :
\(\frac{x+18}{2018}+\frac{x+17}{2017}+\frac{x+16}{2016}=3\)
\(\Leftrightarrow\)\(\left(\frac{x+18}{2018}-1\right)+\left(\frac{x+17}{2017}-1\right)+\left(\frac{x+16}{2016}-1\right)=3-3\) ( trừ hai vế cho 3 )
\(\Leftrightarrow\)\(\frac{x-2000}{2018}+\frac{x-2000}{2017}+\frac{x-2000}{2016}=0\)
\(\Leftrightarrow\)\(\left(x-2000\right)\left(\frac{1}{2018}+\frac{1}{2017}+\frac{1}{2016}\right)=0\)
Vì \(\frac{1}{2018}+\frac{1}{2017}+\frac{1}{2016}\ne0\)
Nên \(x-2000=0\)
\(\Rightarrow\)\(x=2000\)
Vậy \(x=2000\)
Chúc bạn học tốt ~


B1:Tính số số hạng của dãy số:(2018 - 16) :1+1=2003(số số hạng)
B2:Tìm số hạng ở giữa dãy số:2018:2=1001
B3:Tính tích dãy số:2003.1001=4044091051

Lời giải:
a.
PT $\Leftrightarrow (x+3)^2=2016^{2020}-17^{91}+9$
Ta thấy: $2016^{2020}-17^{91}+9\equiv 0-(-1)^{91}+0\equiv -1\equiv 2\pmod 3$
Mà 1 scp thì chia $3$ chỉ dư $0$ hoặc $1$ nên pt vô nghiệm.
b.
$x^2=2016(y-1)^2-2017^{2019}\equiv 0-1^{2019}\equiv 3\pmod 4$
Mà 1 scp chia $4$ chỉ dư $0$ hoặc $1$ nên vô lý.
Vậy pt vô nghiệm.
c.
$(x-1)^2=2017^{2017}+1\equiv 1^{2017}+1\equiv 2\pmod 4$
Mà 1 scp khi chia cho $4$ chỉ dư $0$ hoặc $1$ nên vô lý
Vậy pt vô nghiệm
d.
$(x+2)^2=2018^{10}+4\equiv (-1)^{10}+1\equiv 2\pmod 3$
Mà 1 scp khi chia $3$ dư $0$ hoặc $1$ nên vô lý
Vậy pt vô nghiệm.

a) Ta có : \(16^{17}=\left(2^4\right)^{17}=2^{68}\)
\(8^{18}=\left(2^3\right)^{18}=2^{54}\)
Vì \(2^{68}>2^{54}\Rightarrow16^{17}>8^{18}\)
b) Ta có: \(3^{555}=\left(3^5\right)^{111}=243^{111}\)
\(5^{333}=\left(5^3\right)^{111}=125^{111}\)
Vì \(243^{111}>125^{111}\Rightarrow3^{555}>5^{333}\)
c) Ta có : \(2017^2=2017\cdot2017=2017\cdot2016+2017\)
\(2016\cdot2018=2016\cdot\left(2017+1\right)=2016\cdot2017+2016\)
Vì 2016 < 2017 nên 2016*2017 + 2017 > 2016*2017 + 2016
Vậy \(2017^2>2016\cdot2018\)
Lưu ý : dấu \(\left(\cdot\right)\)là dấu nhân nha bạn

a) \(x^{2017}=8x^{2017}\)
\(\Rightarrow8x^{2017}-x^{2017}=0\)
\(\Rightarrow7x^{2017}=0\)
\(\Rightarrow x^{2017}=0\)
\(\Rightarrow x=0\)
Vậy x = 0
b) \(x^{2016}=16x\)
\(\Rightarrow16x-x^{2016}=0\)
\(\Rightarrow x\left(16-x^{2015}\right)=0\)
\(\Rightarrow\left[\begin{matrix}x=0\\16-x^{2015}=0\end{matrix}\right.\Rightarrow\left[\begin{matrix}x=0\left(chọn\right)\\x^{2015}=16\left(loại\right)\end{matrix}\right.\)
Vậy x = 0

a, TK: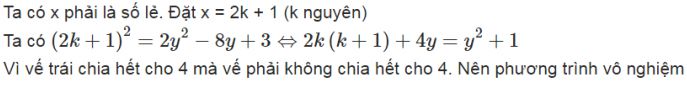
(x lẻ do \(2y^2-8y+3=2\left(y^2-4y\right)+3=x^2\) lẻ)
\(b,\Leftrightarrow\left(x^2-4x+4\right)+\left(y^2+4y+4\right)=9\\ \Leftrightarrow\left(x-2\right)^2+\left(y+2\right)^2=9\)
Vậy pt vô nghiệm do 9 ko phải tổng 2 số chính phương

\(A=1\dfrac{1}{15}.1\dfrac{1}{16}.1\dfrac{1}{17}......1\dfrac{1}{2016}.1\dfrac{1}{2017}\)
\(A=\dfrac{16}{15}.\dfrac{17}{16}.\dfrac{18}{17}......\dfrac{2017}{2016}.\dfrac{2018}{2017}\)
\(A=\dfrac{16.17.18......2017.2018}{15.16.17......2016.2017}\)
\(A=\dfrac{2018}{15}\)