Trong hình bs 11 ta có tam giác EFG và tia Fm .
Chứng minhh rằng :
GEm = EFG + EGF
Giải giúp mình với , ai trả lời nhanh và đúng thì mình tick 5 tick cho
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

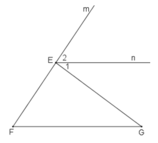
Kẻ tia En song song với FG.
∠F và ∠E2 ở vị trí đồng vị ⇒ ∠F = ∠E2. (1)
∠G và ∠E1 ở vị trí so le trong ⇒ ∠G = ∠E1. (2)
Từ (1) và (2) suy ra: ∠F + ∠G = ∠E1 + ∠E2 (đpcm).
Hay ∠EFG + ∠EGF = ∠GEm.

Tổng 3 góc tam giác = 180 độ => góc FEG = 180 độ - FEG - EGF
Mà FEG và GEm bù nhau => FEG = 180 độ - GEm => EFG + EGF = GEm

Gọi ƯCLN (2n+1;6n+5) = d ( d thuộc N sao )
=> 2n+1 và 6n+5 đều chia hết cho d
=> 3.(2n+1) và 6n+5 đều chia hết cho d
=> 6n+3 và 6n+5 đều chia hết cho d
=> 6n+5-(6n+3) chia hết cho d
=> 2 chia hết cho d
Mà 2n+1 lẻ nên d lẻ
=> d=1
=> ƯCLN (2n+1;6n+5) = 1
=> ĐPCM
k mk nha
Gọi UCLN(2n+1;6n+5)=d
Ta có: 2n+1 chia hết cho d\(\Rightarrow3\left(2n+1\right)\) chia hết cho d\(\Rightarrow6n+3\) chia hết cho d
6n+5 chia hết cho d
\(\Rightarrow\left(6n+5\right)-\left(6n+3\right)\) chia hết cho d
\(\Rightarrow2\) chia hết cho d
\(\Rightarrow d\in\left\{1,2\right\}\).Vì 2n+1 lẻ nên không chia hêt cho 2
\(\Rightarrowđpcm\)

Đáy bé của vườn trường là:
60 x \(\frac{2}{3}\)= 40( m)
a) Diện tích vườn trường là:
( 60 + 40) x 9 : 2 = 450( m2)
Độ dài đáy của mảnh vườn hình tam giác là:
60 - 40 = 20( m)
b) Diện tích mảnh vườn hình tam gics là:
20 x 40 : 2 = 400( m2)
Đ/S: a) 450 m2; b) 400 m2

Bài giải
Ta có : \(BC\text{ }//\text{ }Az\) nên \(\widehat{C_2}=\widehat{A_2}\) ( hai góc so le trong )
Mà \(\widehat{CAx}=\widehat{A_2}+\widehat{A_3}\) là góc ngoài tại đỉnh A của \(\Delta ABC\) nên \(\widehat{A_2}+\widehat{A_3}=\widehat{B}+\widehat{C_2}\)
lại có : \(\widehat{B}=\widehat{C_2}=\widehat{A_2}\) nên \(\widehat{A_3}=\widehat{B}=\widehat{C_2}=\widehat{A_2}\)
Vì \(\widehat{A_2}=\widehat{A_3}\) nên Az là tia phân giác \(\widehat{CAx}\)
Cậu cầu cứu ai đi ....😅😅😅😅
Tớ cũng đg tìm bài này ...hehe 😁😁😁😁
EFG
+
EGF
=
GEm
suy ra G+F=m dư 1
m+1=E
mình nói đến đây thôi nha vì mình học lớp 6