Biết rằng x + y = 2. Chứng minh
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




1. Ta chọn $x=3k;y=4k;z=5k$ với $k$ là số nguyên dương.
Khi này $x^2+y^2=25k^2 =z^2$. Tức có vô hạn nghiệm $(x;y;z)=(3k;4k;5k)$ với $k$ là số nguyên dương thỏa mãn

mong có người giải bài này cho bạn mình cũng đang tìm bài này nhưng chưa ai giải đc

Đề sai rồi em, đề đúng phải là:
\(ab\left(x^2+y^2\right)+xy\left(a^2+b^2\right)=ab\)
Vế phải em thiếu a

a) Ta có:
VT = (x - y)² + 4xy
= x² - 2xy + y² + 4xy
= x² + 2xy + y²
= (x + y)²
= VP
b) Ta có:
(x + y)² = (x - y)² + 4xy
= 5² + 4.3
= 25 + 12
= 37

Ta có:
\(x^2=\left|x\right|^2\)
\(y^2=\left|y\right|^2\)
Mà: \(x>y\Rightarrow\left|x\right|< \left|y\right|\) ( Do x,y < 0)
\(\Rightarrow x^2< y^2\)
Tình hình là t học ngu quá nên bị mắng, trượt chuyên rồi :(
Vậy nên chị kiểm soat nick không được ib lung tung :(((
Lời giải : Do vai trò bình đẳng của x và y nên có thể giả sử x ≤ y.
Từ đó => : Do đó
Do đó 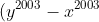.(y%20-%20x)%20%20%5Cgeq%200)

 vào hai vế ta có :
vào hai vế ta có : %20%5Cgeq%20(x+y)%20(x%5E%7B2003%7D%20+%20y%5E%7B2003%7D)%20=%202.(x%5E%7B2003%7D%20+%20y%5E%7B2003%7D))
.)
=> :
Cộng thêm
=> :