Giúp mình với ạ!!! Thank nhiều!!!
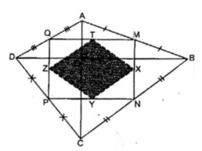
Cho hình vuông ABCD. Gọi M,N,P,Q là các điểm thuộc các cạnh AB,BC,CD,DA. Biết AB = a
Chứng minh rằng: \(2a^2\le MN^2+NP^2+PQ^2+QM^2\le4a^2\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
29 tháng 10 2019
Trong △ ABD ta có:
M là trung điểm của AB
Q là trung điểm của AD nên MQ là đường trung bình của △ ABD.
⇒ MQ // BD và MQ = 1/2 BD (tính chất đường trung bình của tam giác) (1)
Trong △ CBD ta có:
N là trung điểm của BC
P là trung điểm của CD
nên NP là đường trung bình của △ CBD
⇒ NP // BD và NP = 1/2 BD (tính chất đường trung bình của tam giác) (2)
Từ (1) và (2) suy ra: MQ // NP và MQ = NP nên tứ giác MNPQ là hình bình hành
AC ⊥ BD (gt)
MQ // BD
Suy ra: AC ⊥ MQ
Trong △ ABC có MN là đường trung bình ⇒ MN // AC
Suy ra: MN ⊥ MQ hay (NMQ) = 90 0
Vậy tứ giác MNPQ là hình chữ nhật.
24 tháng 10 2021
TL
Mik ko có hình cả sai mik sorry nha
Độ dài cạnh AM là:
8:2=4(cm)
Độ dài cạnh AM cũng chính là độ dài của cạnh MB,BN,NC.
Diện tích hình tam giác AMD là :
4x8:2=16(cm2)
Diện tích hình tam giác NCD là:
8x4:2=16(cm2)
Diện tích hình tam giác MBN là:
4x4:2=8(cm2)
Diện tích hình vuông ABCD là :
8x8=64(dm2)
Diện tích hình tam giác MND là :
64-(8+16 + 16)=24(dm2)
Đáp số:24dm2
Hok tốt
