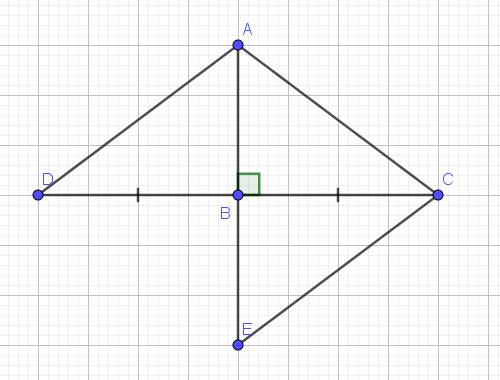
Cho ABC vuông tại B. Trên tia đối của tia BC lấy điểm D sao cho BD = BC.
a, Chứng minh ABD = ABC
b, Qua C kẻ đường thẳng song song với AD, đường thẳng này cắt tia AB tại E. Chứng minh ACE là tam giác cân.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét hai tam giác vuông: \(\Delta ABD\) và \(\Delta ABC\) có:
AB chung
BD = BC (gt)
\(\Rightarrow\Delta ABD=\Delta ABC\) (hai cạnh góc vuông)
b) Do \(\Delta ABD=\Delta ABC\) (cmt)
\(\Rightarrow\widehat{ADB}=\widehat{ACB}\) (hai góc tương ứng)
Ta có: CE // AD (gt)
\(\Rightarrow\widehat{BCE}=\widehat{ADB}\) (so le trong)
\(\Rightarrow\widehat{BCE}=\widehat{ACB}\)
Xét hai tam giác vuông: \(\Delta CBA\) và \(\Delta CBE\) có:
BC là cạnh chung
\(\widehat{ACB}=\widehat{BCE}\) (cmt)
\(\Rightarrow\Delta CBA=\Delta CBE\) (cạnh góc vuông-góc nhọn kề)
\(\Rightarrow CA=CE\) (hai cạnh tương ứng)
\(\Delta ACE\) có CA = CE (cmt)
\(\Rightarrow\Delta ACE\) cân tại C

a: Xét ΔCAB vuông tại A và ΔCAD vuông tại A có
CA chung
AB=AD
Do đó: ΔCAB=ΔCAD
=>CB=CD
=>ΔCBD cân tại C
b: Ta có: \(\widehat{EAC}=\widehat{DCA}\)(hai góc so le trong, AE//CD)
\(\widehat{ECA}=\widehat{DCA}\)(ΔDCA=ΔBCA)
Do đó: \(\widehat{EAC}=\widehat{ECA}\)
=>ΔEAC cân tại E
c: Ta có: \(\widehat{EAC}+\widehat{EAB}=\widehat{BAC}=90^0\)
\(\widehat{ECA}+\widehat{EBA}=90^0\)(ΔABC vuông tại A)
mà \(\widehat{EAC}=\widehat{ECA}\)
nên \(\widehat{EAB}=\widehat{EBA}\)
=>EA=EB
mà EA=EC(ΔEAC cân tại E)
nên EB=EC
=>E là trung điểm của BC

Mk thấy đề sai hay sao ý ko có đường thẳng nào đi qua B song song vs CD và cắt DM cả
mik thấy cô ghi đè s mik ghi lại y chang chứ mik ko bik j cả. mik đọc cx thấy sai sai cái j á mà ko bik mik đọc đè đúng hay là sai nên mik mới đăng
a) Do BD = BC và ∠BDA = ∠BCA = 90° nên ta có tam giác ABD = tam giác ABC (theo định lý góc - cạnh - góc).
=> Vậy, tam giác ABD = tam giác ABC.
b) Do CE // AD và AC cắt CE tại E nên ta có ∠CAE = ∠DAE.
- Do tam giác ABD = tam giác ABC nên AB = AD.
- Vì vậy, tam giác ADE là tam giác cân tại D, tức là AE = DE.
- Do tam giác ABD = tam giác ABC nên AC = BC.
- Vì vậy, tam giác BCE là tam giác cân tại B, tức là BE = CE.
- Do AE = DE và BE = CE nên AC = CE.
=> Vậy, ACE là tam giác cân.
a: Xét ΔABC vuông tại B và ΔABD vuông tại B có
AB chung
BC=BD
Do đó: ΔABC=ΔABD
b: Ta có: CE//AB
=>\(\widehat{CEA}=\widehat{DAB}\)
mà \(\widehat{DAB}=\widehat{CAB}\)(ΔABC=ΔABD)
nên \(\widehat{CAE}=\widehat{CEA}\)
=>ΔCAE cân tại C