Cho mình hỏi phương pháp hệ số bất định có nghĩa là gì?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



PHƯƠNG PHÁP HỆ SỐ BẤT Đ̣NH
Phương pháp giải toán dựa trên cơ sở tính toán và biến đổi hệ số của đa thức người ta gọi là phương pháp hệ số bất đ̣nh. Phương pháp này được sử dụng rất tiện lợi khi giải toán về chia hết , phân tích thành nhân tử và rút gọn biểu thức


- Lực căng bề mặt: là lực tác dụng lên một đoạn đường nhỏ bất kì trên bề mặt chất lỏng luôn có phương vuông góc với đoạn đường này và tiếp tuyến với bề mặt chất lỏng, có chiều làm giảm diện tích bề mặt chất lỏng và có độ lớn f tỉ lệ thuận với độ dài l của đoạn đường đó: f = σl.
σ là hệ số căng bề mặt (suất căng bề mặt), đơn vị N/m.
Giá trị của σ phụ thuộc vào nhiệt độ và bản chất của chất lỏng: σ giảm khi nhiệt độ tăng.
- Phương pháp xác định:
Nhúng đáy vòng chạm vào mặt chất lỏng, rồi kéo lên mặt thoáng. Khi đáy vòng vừa được nâng lên trên mặt thoáng, nó không bị bứt ngay ra khỏi chất lỏng: một màng chất lỏng xuất hiện, bám quanh chu vi ngoài và chu vi trong của vòng, có khuynh hướng kéo vòng vào chất lỏng. Lực Fc do màng chất lỏng tác dụng vào vòng đúng bằng tổng lực căng bề mặt của chất lỏng tác dụng lên chu vi ngoài và chu vi trong của vòng.
Do vòng bị chất lỏng dính ướt hoàn toàn, nên khi kéo vòng lên khỏi mặt thoáng và có một màng chất lỏng căng giữa đáy vòng và mặt thoáng, thì lực căng Fc có cùng phương chiều với trọng lực P của vòng. Giá trị lực F đo được trên lực kế bằng tổng của hai lực này:
F = Fc + P
Đo P và F ta xác định được lực căng bề mặt Fc tác dụng lên vòng.
- Công thức thực nghiệm xác định hệ số căng bề mặt:
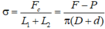

lấy tạm 1 ví dụ thôi nhé!
Giải phương trình \(\sqrt{x-1}+\sqrt{3-x}+4x\sqrt{2x}=x^3+10\)
ĐK: \(1\le x\le3\)
\(\sqrt{x-1}=\frac{1}{2}.2.1.\sqrt{x-1}\le\frac{1}{2}\left(1+x-1\right)=\frac{1}{2}.x\) ( Cô - si )
\(\sqrt{3-x}=\frac{1}{2}.2.1.\sqrt{3-x}\le\frac{1}{2}\left(1+3-x\right)=2-\frac{1}{2}x\)
\(4x\sqrt{2x}=2.2.\sqrt{2}.\sqrt{x^3}\le8+x^3\)
\(\Rightarrow\sqrt{x-1}+\sqrt{3-x}+4x\sqrt{2x}\le x^3+10\)
Dấu "=" khi \(\hept{\begin{cases}1=\sqrt{x-1}\\1=\sqrt{3-x}\\2\sqrt{2}=\sqrt{x^3}\end{cases}\Leftrightarrow x=2}\left(tmđk\right)\)

Phương pháp đồng nhất hệ số (phương pháp hệ số bất định) có cơ sở như sau:
Hai đa thức (dạng thu gọn ) là đồng nhất khi và chỉ khi mọi hệ số của các đơn thức đồng dạng trong hai đa thức phải bằng nhau
VD ax^2+bx+c=2x^2+5x+3 trong đó a,b,c là hằng số, x là ẩn
Từ đó suy ra
a=2, b=5, c=3
Chúc bạn học tốt!!!
Phương pháp hệ số bất định là một phương pháp hay để giải các Pt vô tỉ hoặc phân tích đa thức thành nhân tử - 2 dạng toán cơ bản ở lớp 9. Trong chuyên đề sách nâng cao và PT lớp 8 Tập 1/45 của nhà toán Vũ Hữu Bình đề cập đến phương pháp này.
k di bn