 a. Biết AB = 12 cm , BC = 20 cm. Tính AC, MC
a. Biết AB = 12 cm , BC = 20 cm. Tính AC, MC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: BC=căn 12^2+16^2=20cm
Xét ΔABC vuông tại A có sin C=AB/BC=3/5
=>góc C=37 độ
=>góc B=53 độ
b: AM=12*16/20=9,6cm
BM=AB^2/BC=7,2cm
c: ΔAMB vuông tại M có ME là đường cao
nên AE*AB=AM^2
=>AE*AB=AC^2-MC^2

P/s : bổ sung đề : Thêm đường cao AH ( H thuộc BC )
Giải :
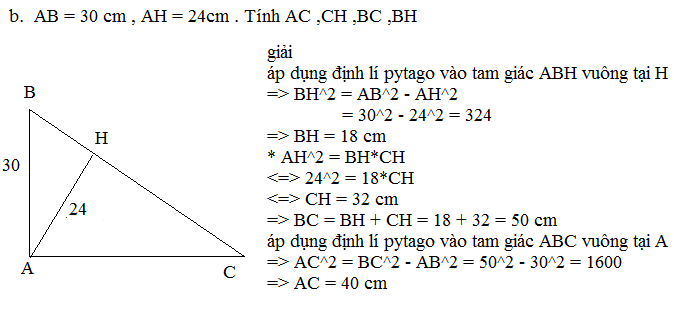
+) Áp dụng định lí pi - ta - go vào tam giác ABC vuông tại A , ta có :
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow AC^2=BC^2-AB^2\)
\(\Leftrightarrow AC=\sqrt{20^2-12^2}=16\left(cm\right)\)
+) Áp dụng hệ thức giữa cạnh và đường cao trong tam giác ABC vuông tại A , đường cao AH , ta có :
+) \(AB^2=BC.HB\)
\(\Leftrightarrow12^2=20HB\)
\(\Leftrightarrow HB=7,2\left(cm\right)\)
\(\Rightarrow HC=BC-HB=20-7,2=12,8\left(cm\right)\)
+) \(AH^2=HB.HC\)
\(\Leftrightarrow AH^2=7,2.12,8\)
\(\Leftrightarrow AH^2=92,16\)
\(\Leftrightarrow AH=9,6\left(cm\right)\)

Bài 1:
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=5^2+12^2=169\)
hay BC=13cm
Ta có: ΔABC vuông tại A
nên bán kính đường tròn ngoại tiếp ΔABC là một nửa của cạnh huyền BC
hay \(R=\dfrac{BC}{2}=\dfrac{13}{2}=6.5\left(cm\right)\)
Bài 2:
Ta có: ABCD là hình thang cân
nên A,B,C,D cùng thuộc 1 đường tròn\(\left(đl\right)\)
hay bán kính đường tròn ngoại tiếp ΔABC cũng là bán kính đường tròn ngoại tiếp tứ giác ABCD
Xét ΔABC có
\(BC^2=AB^2+AC^2\)
nên ΔABC vuông tại A
Suy ra: Bán kính của đường tròn ngoại tiếp tứ giác ABCD là \(R=\dfrac{BC}{2}=10\left(cm\right)\)

Bài 5:
Ta có: \(AB^2=BH\cdot BC\)
\(\Leftrightarrow BH\left(BH+9\right)=400\)
\(\Leftrightarrow BH^2+25HB-16HB-400=0\)
\(\Leftrightarrow BH=16\left(cm\right)\)
hay BC=25(cm)
Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(\left\{{}\begin{matrix}AC^2=CH\cdot BC\\AH\cdot BC=AB\cdot AC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AC=15\left(cm\right)\\AH=12\left(cm\right)\end{matrix}\right.\)

Tam giác ABC là: 16 x 12 : 2 = 96 cm2
MC = 4/16 AC = 1/4 AC
Kẻ thêm từ M đến B, ta có SBAM = 3/4 SABC (vì AM = 3/4 AC, chung chiều cao hạ từ B xuống AC)
=> SBAM = 96 : 4 x 3 = 72 cm2
AM là: 16 - 4 = 12 cm
=> MN là: 72 x 2 : 12 = 12 cm
SMNBC = (12 + 12) x 4 : 2 = 48 (cm2)

Tam giác ABC là: 16 x 12 : 2 = 96 cm2
MC = 4/16 AC = 1/4 AC
Kẻ thêm từ M đến B, ta có SBAM = 3/4 SABC (vì AM = 3/4 AC, chung chiều cao hạ từ B xuống AC)
=> SBAM = 96 : 4 x 3 = 72 cm2
AM là: 16 - 4 = 12 cm
=> MN là: 72 x 2 : 12 = 12 cm
SMNBC = (12 + 12) x 4 : 2 = 48 (cm2)

a: \(BC=\sqrt{8^2+20^2}=4\sqrt{29}\left(cm\right)\)
AB<AC<BC
=>góc C<góc B<góc A
b: Xét ΔCDB có
CA,DK là trung tuyến
CA cắt DK tại M
=>M là trọng tâm
=>CM=2/3*CA=2/3*20=40/3(cm)

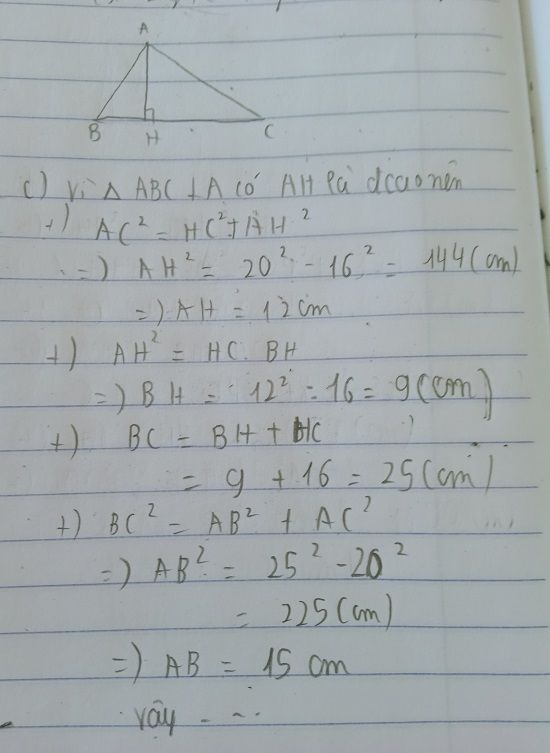
a: Ta có;ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(AC^2+12^2=20^2\)
=>\(AC^2=20^2-12^2=256=16^2\)
=>AC=16(cm)
Xét ΔBAC có BM là phân giác
nên \(\dfrac{AM}{AB}=\dfrac{CM}{CB}\)
=>\(\dfrac{AM}{12}=\dfrac{CM}{20}\)
=>\(\dfrac{AM}{3}=\dfrac{CM}{5}\)
mà AM+CM=AC=16cm
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{AM}{3}=\dfrac{CM}{5}=\dfrac{AM+CM}{3+5}=\dfrac{16}{8}=2\)
=>\(CM=2\cdot5=10\left(cm\right)\)
b: Ta có: MI\(\perp\)BC
AK\(\perp\)BC
Do đó: MI//AK
Xét ΔCAK có MI//AK
nên \(\dfrac{CI}{IK}=\dfrac{CM}{MA}\)
mà \(\dfrac{CM}{MA}=\dfrac{CB}{BA}\)
nên \(\dfrac{CI}{IK}=\dfrac{CB}{BA}\)
=>\(AB\cdot IC=IK\cdot BC\)