Tìm a để đa thức x3-3x2+5x+a chia hết cho đa thức x-2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: \(\Leftrightarrow2x^4-2x^3+2x^2+3x^3-3x^2+3x-2x^2+2x+2+a-2⋮x^2-x+1\)
=>a=2

\(\Leftrightarrow x^3+3x^2+5x+a=\left(x+3\right)\cdot a\left(x\right)\)
Thay \(x=-3\Leftrightarrow-27+27-15+a=0\Leftrightarrow a=15\)

b: \(=\dfrac{2x^4-2x^3-2x^2-3x^3+3x^2+3x+x^2-x-1}{x^2-x-1}\)
\(=2x^2-3x+1\)

Bài 1:
a: \(=\dfrac{2x^4-8x^3+2x^2+2x^3-8x^2+2x+18x^2-72x+18+56x-15}{x^2-4x+1}\)
\(=2x^2+2x+18+\dfrac{56x-15}{x^2-4x+1}\)

\(\Leftrightarrow x^3-4x^2+x^2-2x+7x-14+15⋮x-2\)
\(\Leftrightarrow x-2\in\left\{1;-1;3;-3;5;-5;15;-15\right\}\)
hay \(x\in\left\{3;1;5;-1;7;-3;17;-13\right\}\)

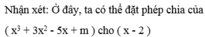
để tìm số dư, rồi cho số dư đó bằng 0, từ đó tìm được giá trị của m.
Mở rộng: Bài toán này ta áp dụng phân tích đa thức thành nhân tử để giải toán


Bài 1:
Ta có: \(5x^3-3x^2+2x+a⋮x+1\)
\(\Leftrightarrow5x^3+5x^2-8x^2-8x+10x+10+a-10⋮x+1\)
\(\Leftrightarrow a-10=0\)
hay a=10
\(f\left(x\right)=x^3-3x^2+5x+a\)
theo định lý Bezout, số dư của đa thức f(x) cho nhị thức x-2 là f(2)
ta có f(2)=\(2^3-3.2^2+5.2+a\)
= \(6+a\)
Có số dư của f(x) cho x-2 là 6+a => để trở thành phép chia hết <=> 6+a=) => a=-6