Bài 1 : Cho 2 đg thẳng (d1) : y = 2x + 1 và ( d2 ) : y = x + 1
a, CM 2 đg thẳng cắt nhau
b, CM giao điểm của 2 đg thẳng là điểm M(0;1)
c, Vẽ 2 đg thẳng trên cùng 1 hệ trục toạ độ
d, Tính S tam giác tạo bởi Mvà 2 giao điểm của các đg thẳng với trục hoành .
Vẽ hình minh hoạ giúp mình nữa với ai làm đc mình tick cho 5 tick

a: Vì \(2\ne1\) nên (d1) cắt (d2)
b: Tọa độ giao điểm của (d1) và (d2) là:
\(\left\{{}\begin{matrix}2x+1=x+1\\y=x+1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x-x=1-1\\y=x+1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=0+1=1\end{matrix}\right.\)
Vậy: (d1) giao (d2) tại M(0;1)
c: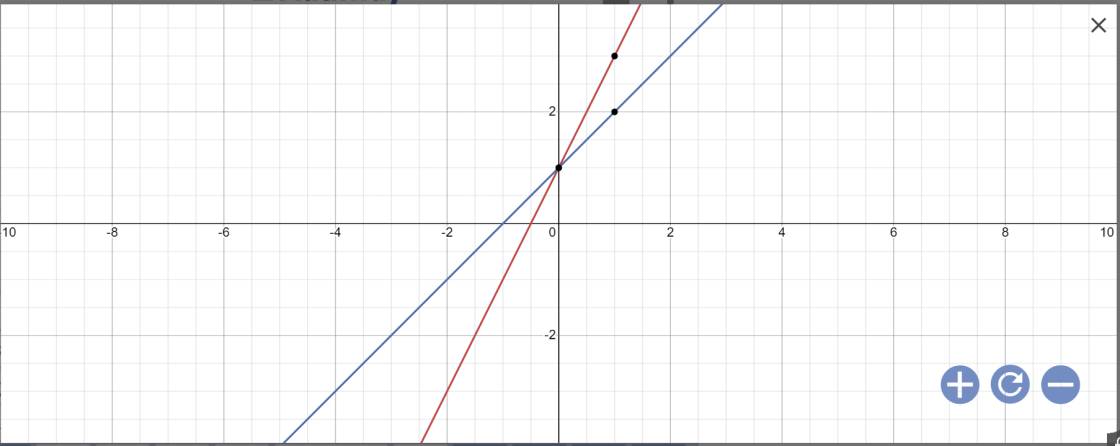
d: Gọi A,B lần lượt là giao điểm của (d1),(d2) với trục Ox
Tọa độ A là:
\(\left\{{}\begin{matrix}y=0\\2x+1=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\x=-\dfrac{1}{2}\end{matrix}\right.\)
Tọa độ B là:
\(\left\{{}\begin{matrix}y=0\\x+1=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\x=-1\end{matrix}\right.\)
Vậy: M(0;1); A(-0,5;0); B(-1;0)
\(MA=\sqrt{\left(-0,5-0\right)^2+\left(0-1\right)^2}=\dfrac{\sqrt{5}}{2}\)
\(MB=\sqrt{\left(-1-0\right)^2+\left(0-1\right)^2}=\sqrt{2}\)
\(AB=\sqrt{\left(-1+0,5\right)^2+\left(0-0\right)^2}=0,5\)
Xét ΔMAB có \(cosAMB=\dfrac{MA^2+MB^2-AB^2}{2\cdot MA\cdot MV}=\dfrac{\dfrac{5}{4}+2-0,25}{2\cdot\dfrac{\sqrt{5}}{2}\cdot\sqrt{2}}=\dfrac{3}{\sqrt{10}}\)
=>\(sinAMB=\sqrt{1-\left(\dfrac{3}{\sqrt{10}}\right)^2}=\dfrac{1}{\sqrt{10}}\)
Diện tích tam giác AMB là:
\(S_{AMB}=\dfrac{1}{2}\cdot MA\cdot MB\cdot sinAMB\)
\(=\dfrac{1}{2}\cdot\dfrac{1}{\sqrt{10}}\cdot\dfrac{\sqrt{5}}{2}\cdot\sqrt{2}=\dfrac{1}{4}\)
Giúp mình đi mn