A, B, C là ba điểm tạo thành một tam giác vuông tại A, trong điện trường đều có vectơ cường độ điện trường song song với cạnh AB, chiều từ A đến B và có độ lớn E = 104 V/m. Cho AB = AC = 5 cm. Một prôtôn (có điện tích 1,6.10−19 C) dịch chuyển từ A đến B rồi từ B đến C. Tính công của lực điện tác dụng lên electron trong hai trường hợp trên.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: \(q_e=-1,6\cdot10^{-19}C\)
\(m_e=9,1\cdot10^{-31}kg\)
Vật chuyển động ngược chiều điện trường nên:
\(A=W_{đ1}-W_{đ2}\)\(\Rightarrow F_d\cdot d=\dfrac{1}{2}mv^2-0\)
\(\Rightarrow\left|-q\right|\cdot E\cdot d=\dfrac{1}{2}mv^2\)
\(\Rightarrow v=\sqrt{\dfrac{2qEd}{m}}=\sqrt{\dfrac{2\cdot1,6\cdot10^{-19}\cdot3000\cdot0,02}{9,1\cdot10^{-31}}}=4,6\cdot10^6\)m/s

Chọn đáp án B
Gọi H là hình chiếu của C xuống cạnh AB, tức CH là đường cao kẻ từ đỉnh C của tam giác vuông CAB
Hiệu điện thế giữa hai điểm A và C là:


a. Vì E → hướng từ A đến C, ta có: U A C = E . A C = 5000 . 0 , 04 = 200 V
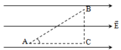
→ U C B = A C B q = 0 do → C B → ⊥ E →
→ U A B = U A C + U C B = 200 V hoặc ta tính theo cách khác: → U A B = E . A B ¯ . cos α = 200
b. Công của lực điện khi electron di chuyển từ A đến B là:
→ A A B = q U A B = − 1 , 6.10 − 19 .200 = − 3 , 2.10 − 17 J

\(\overrightarrow{A_{AC}}=q.\overrightarrow{E_{AC}}.\overrightarrow{AC}\Rightarrow A_{AC}=-1,6.10^{-19}.3000.0,08=...\left(J\right)\)
\(\overrightarrow{A_{BC}}=q.\overrightarrow{E_{BC}}.\overrightarrow{BC}=-1,6.10^{-19}.3000.0,06.\cos90^0=...\left(J\right)\)

Chọn A
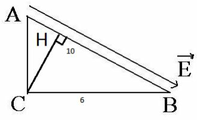
U A B =E.AB=5. 10 5 .10/100=5. 10 4 V
U B C = - U C B =-E.d(B,CH)=-E.BH=-E. B C 2 /AB=-5. 10 5 .36. 10 - 4 /(10. 10 - 2 )= -18000V

a) Hiệu điện thế:
- Vì điểm A và B nằm trên cùng một mặt phẳng thế nên điện thế giữa hai điểm đó là như nhau, do đó: UAB = 0.
- Ta có UAC = E.AC = 1000.0,08 = 80 V.
- Tương tự:UBC=E.AC=1000.0,08=80V.UBC=E.AC=1000.0,08=80V.b) Lực điện trường là loại lực thế nên công của chúng không phụ thuộc vào đường đi, do đó:
A=|e|UBC=|e|UACA=|e|UBC=|e|UAC=1,6.10−19.80=12,8.10−18J.=1,6.10−19.80=12,8.10−18J.c) Công của lực điện trường bằng độ biến thiên động năng của êlectron:
AAC=mv2C//2−mv20/2
⇒vC=√2AACm=√2.128.10−199,1.10−31⇒vC=2AACm=2.128.10−199,1.10−31≈5,3.106m/s.



Từ A đến B:
$W_{AB} = 1.6 \times 10^{-19} \, \text{C} \cdot 10^4 \, \text{V/m} \cdot 0.05 \, \text{m} = 8 \times 10^{-18} \, \text{J}$
Từ B đến C: Do cường độ điện trường song song với cạnh AB, nên khi prôtôn dịch chuyển từ B đến C, công do lực điện tác dụng lên prôtôn sẽ bằng 0 (vì góc giữa cường độ điện trường và hướng dịch chuyển là 90 độ).
=> Tổng công của lực điện tác dụng lên prôtôn khi nó dịch chuyển từ A đến B rồi từ B đến C là $8 \times 10^{-18}$ J.