tứ giác ABCD nọi tiếp đường tròn đường kính AC,biết DBC=55độ.Số đo góc ACD =?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


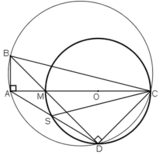
a) 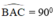 ⇒ A ∈ đường tròn đường kính BC.
⇒ A ∈ đường tròn đường kính BC.
D ∈ đường tròn đường kính MC

⇒ D ∈ đường tròn đường kính BC
⇒ A, B, C, D cùng thuộc đường tròn đường kính BC
hay tứ giác ABCD nội tiếp.
b) Xét đường tròn đường kính BC:
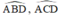 đều là góc nội tiếp chắn cung
đều là góc nội tiếp chắn cung 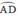
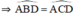
c) + Trong đường tròn đường kính MC:
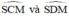 đều là các góc nội tiếp cùng chắn cung
đều là các góc nội tiếp cùng chắn cung 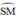
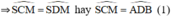
+ Trong đường tròn đường kính BC:
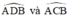 đều là các góc nội tiếp chắn cung
đều là các góc nội tiếp chắn cung 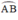
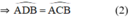


Ta có : \(sd\widebat{AB}=2.sd\widehat{ADB}=2.15^o=30^o\) ( sd cung bằng hai lần góc nội tiếp chắn cung đó )
: \(sd\widebat{CD}=2.\widehat{DBC}=2.30^o=60^o\) ( sd cũng bằng hai lần góc nội tiếp chắn cung đó )
Ta co : \(sd\widebat{AD}\)+ \(sd\widebat{BC}\)+\(sd\widebat{AB}\)+ \(sd\widebat{CD}\) \(=360^o\)
=> \(sd\widebat{AD}+sd\widebat{BC}=360^o-\left(sd\widebat{AB}+sd\widebat{CD}\right)\)
\(=360^o-\left(30^o+60^o\right)=270^o\)
Ta có : \(sd\widehat{BIC}=\frac{1}{2}\left(sd\widebat{AD}+sd\widebat{BC}\right)=\frac{1}{2}.270^o=135^o\)( góc có đỉnh ở bên trong đường trong bằng nửa tổng số đo hai cung bị chắn )

2:
a: góc MAO+góc MBO=180 độ
=>MAOB nội tiếp
b: ΔONP cân tại O
mà OK là trung tuyến
nên OK vuông góc NP
góc OKM=góc OAM=góc OBM=90 độ
=>O,P,A,M,B cùng nằm trên đường tròn đường kính OM
góc AKM=góc AOM
góc BKM=góc BOM
mà góc AOM=góc BOM
nên góc AKM=góc BKM
=>KM là phân giác của góc AKB

c) HC=1/2*BC=12
=>AH=căn(20^2-12^2)=16
ta có Sin(BAO)=12/20=>BAO=36.86989765
=>AOB=180-36.86989765*2=106.2602047
Ta có AB^2=AO^2+OB^2-2*OB*OA*cos(106.2602047)
<=>AO^2+OA^2-2OA^2*cos(106.2602047)=20^2
=>OA=12.5
a) ta có DOC=cung DC
Vì DOC là góc ở tâm và DAC là góc chắn cung DC
=>DOC=2*AOC (1)
mà tam giác AOC cân =>AOC=180-2/AOC (2)
từ (1);(2) ta dc DOC+AOC=180
b)góc ACD là góc nội tiếp chắn nữa đường tròn
=>ACD=90 độ
c) đợi xí

a, ta có ^BAC=900(góc nội tiếp chắn nửa đường tròn đường kính BC)
^MDC=900(góc nội tiếp chắn nửa đường tròn đường kính MC)
=>^BAC=^MDC(=900)
=>tứ giác ABCD nội tiếp (hai đỉnh A và D kề nhau cùng nhìn cạnh BC dưới hai góc bằng nhau)
b. vì tứ giác ABCD nội tiếp (câu a) nên ^ABD=^ACD (hai góc nội tiếp cùng chắn cung AD)
c, ta có bốn điểm D,S,C,M cùng thuộc đường tròn đường kính MC
=>tứ giác DSCM nội tiếp
=>^ADM=^SCM (cùng bù với ^MDS)
Mà ADCB nội tiếp nên ^ADM=^MCB( hai góc nội tiếp cùng chắn cung AB)
Do đó ^SCM=^MCB
=>CA là tia phân giác ^SCB
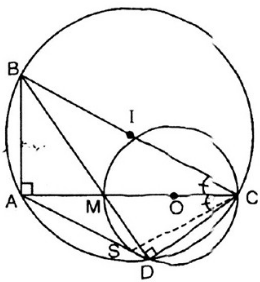

TA có \(\widehat{DBC}=55^0\Rightarrow sđ\widebat{CD}=110^0\)
Mà AC là đường kính nên \(sđ\widebat{AD}=180^0-110^0=70^0\Rightarrow\widehat{ACD}=\frac{1}{2}sđ\widebat{AD}=35^0\)