một tổ công nhân dc giao sản xuất 4000 sản phẩm vs năng suất đã định trc.Trong 10 ngày đầu tổ đã sản xuất đúng tiến độ.Thời gian sau , mỗi ngày tỏ sản xuất tăng thêm 20 sản phẩm nên đã hoàn thành kế hoạch sớm hơn 5 ngày . Tính năng suất định trc
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
14 tháng 4 2017
Gọi số sản phẩm tổ dự định làm theo kế hoạch là x (sản phẩm, 
).
Thiết lập được PT:
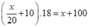
Từ đó tìm được x = 800 (sản phẩm)
AH
Akai Haruma
Giáo viên
22 tháng 7 2021
Lời giải:
Gọi thời gian dự kiến là $a$ ngày thì năng suất dự kiến là $\frac{130}{a}$ sản phẩm / ngày.
Theo bài ra ta có:
Năng suất thực tế: $\frac{130}{a}+2$
Thời gian thực tế: $a-2$
Sản lượng thực tế: $(\frac{130}{a}+2)(a-2)=130+2$
$\Leftrightarrow a-\frac{130}{a}=3$
$\Leftrightarrow a^2-3a-130=0$
$\Rightarrow a=13$ (chọn) hoặc $a=-10$ (loại)
Vậy thời gian dự kiến là $13$ ngày.
27 tháng 6 2021
Bài 21:
Gọi x (sản phẩm/giờ) là năng suất dự kiến ban đầu của người đó \(\left(x\inℕ^∗\right)\)
=> x + 2 (sản phẩm/giờ) là năng suất lúc sau của người đó
Theo bài ta có phương trình sau:
\(\frac{150}{x}-\frac{1}{2}-2=\frac{150-2x}{x+2}\)
\(\Leftrightarrow300\left(x+2\right)-x\left(x+2\right)-4x\left(x+2\right)=2\left(150-2x\right)x\)
\(\Leftrightarrow300x+600-x^2-2x-4x^2-8x=300x-4x^2\)
\(\Leftrightarrow x^2+10x-600=0\)
\(\Leftrightarrow\left(x-20\right)\left(x+30\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x-20=0\\x+30=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=20\left(tm\right)\\x=-30\left(ktm\right)\end{cases}}\)
Vậy ban đầu năng suất người đó là 20 (sản phẩm/giờ)
27 tháng 6 2021
Bài 22:
Gọi x (sản phẩm/giờ) là năng suất dự kiến của người đó \(\left(x\inℕ^∗;x< 20\right)\)
=> x + 1 (sản phẩm/giờ) là năng suất lúc sau của người đó
Theo bài ra ta có phương trình:
\(\frac{80}{x+1}-\frac{1}{5}=\frac{72}{x}\)
\(\Leftrightarrow400x-x\left(x+1\right)=360\left(x+1\right)\)
\(\Leftrightarrow400x-x^2-x=360x+360\)
\(\Leftrightarrow x^2-39x+360=0\)
\(\Leftrightarrow\left(x-15\right)\left(x-24\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x-15=0\\x-24=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=15\left(tm\right)\\x=24\left(ktm\right)\end{cases}}\)
Vậy năng suất ban đầu là 15 sp/giờ
22 tháng 5 2022
gọi số sản phẩm tổ phải sản xuất theo kế hoạch là : x (x ϵ N*)
→số sản phảm thực tế tổ làm đc là : x+15
theo thực tế thì 1 ngày tổ đó làm đc: 60+5=65(sản phẩm)
ta có, theo thực tế thì tổ đó hoàn thành sản phẩm trước 2 ngày:
→ ta có phương trình
\(\dfrac{x}{60}\)-\(\dfrac{x+15}{65}\)=2
giải hệ phương trình, ta được x=1740(thỏa mãn)
14 tháng 3 2023
Gọi thời gian và số sản phẩm lần lượt là a,b
Theo đề, ta có: b=40a và (a+2)*30=b-10
=>b=40a và 30a+60-b+10=0
=>-40a+b=0 và 30a-b=-70
=>a=7 và b=280
=>Số sản phẩm là 280
NH
18 tháng 4 2020
Thực tế tổ sản xuất làm được số sản phẩm mỗi ngày là: 30 + (30 : 100 x 10) = 33 (sản phẩm)
Gọi số ngày dự định hoàn thành xong tất cả sản phẩm là x (ngày, x > 2)
Số ngày thực tế hoàn thành xong tất cả sản phẩm là x - 2 (ngày)
Tổng số sản phẩm dự định làm được là: 30x (sản phẩm)
Tổng số sản phẩm thực tế làm được là: 33(x - 2) (sản phẩm)
Theo bài ra, ta có pt: 33(x - 2) - 30x = 15
<=> 33x - 66 - 30x = 15
<=> 3x = 15 + 66
<=> 3x = 81
<=> x = 27 (thỏa mãn)
Vậy số lượng sản phẩm mà tổ phải làm theo kế hoạch là 27 . 30 = 810 (sản phẩm)
26 tháng 3 2022
Thực tế tổ sản xuất làm được số sản phẩm mỗi ngày là: 30 + (30 : 100 x 10) = 33 (sản phẩm)
Gọi số ngày dự định hoàn thành xong tất cả sản phẩm là x (ngày, x > 2)
Số ngày thực tế hoàn thành xong tất cả sản phẩm là x - 2 (ngày)
Tổng số sản phẩm dự định làm được là: 30x (sản phẩm)
Tổng số sản phẩm thực tế làm được là: 33(x - 2) (sản phẩm)
Theo bài ra, ta có pt: 33(x - 2) - 30x = 15
<=> 33x - 66 - 30x = 15
<=> 3x = 15 + 66
<=> 3x = 81
<=> x = 27 (thỏa mãn)
Vậy số lượng sản phẩm mà tổ phải làm theo kế hoạch là 27 . 30 = 810 (sản phẩm)