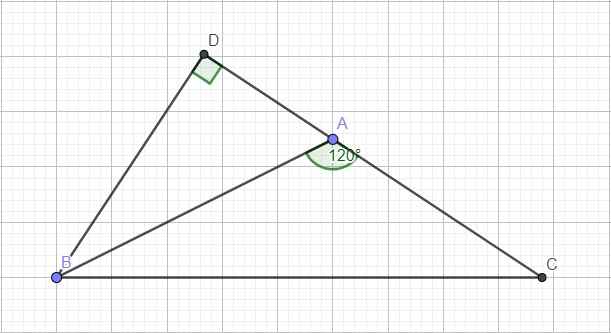
cho hình tam giác ABC có góc A = 120 độ có BC=a, AC=b, AB= C chứng minh a^2=b^2+c^2+b^2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Kẻ CE vuông góc với AB, ta có ngay tam giác ACE vuông có một góc nhọn 60. Suy ra \(AE=\frac{1}{2}AC=\frac{b}{2},CE=\frac{\sqrt{3}}{2}b\). Xét tam giác vuông EBC có '\(EB=c+\frac{b}{2},EC=\frac{\sqrt{3}}{2}b\to a^2=BC^2=BE^2+CE^2=\left(c+\frac{b}{2}\right)^2+\left(\frac{\sqrt{3}}{2}b\right)^2=c^2+bc+b^2\)

theo định lý hàm số cos thì :
\(a^2=b^2+c^2-2bc\)
cos A=\(b^2+c^2-2bc\)
cos 120 mà cos 1200=\(-\frac{1}{2}\)
\(\Rightarrow a^2=b^2+c^2+bc\)

A B C E a b c
Kẻ CE | AB.
Ta có \(\Delta ACE\) vuông tại E có góc A = 60o.
\(\Rightarrow AE=\frac{1}{2}AC=\frac{b}{2}\)
\(CE=AC^2-AE^2=\frac{\sqrt{3}}{2}b\)
Xét \(\Delta EBC\) vuông tại E có :
\(EB=c+\frac{b}{2}\)
\(EC=\frac{\sqrt{3}}{2}b\)
\(\Rightarrow a^2=BC^2=EB^2+EC^2=\left(c+\frac{b}{2}\right)^2+\left(\frac{\sqrt{3}}{2}b\right)^2=b^2+c^2+bc\)
Vậy ...
![[IMG]](http://i1158.photobucket.com/albums/p610/Khiem_Vuong/Untitled-1.png?t=1372301010) - Vẽ CD vuông góc tia AB tại D.
- Vẽ CD vuông góc tia AB tại D.
Ta thấy: \(\widehat{BAC}=120^o\Rightarrow\widehat{CAD}=60^o\left(p.g\right)\)
Tam giác CAD là nửa tam giác đều
\(\Rightarrow AD=\frac{1}{2}AC=\frac{1}{2}AB\)
- Tam giác CDB vuông tại D
\(\Rightarrow BC^2=BD^2+CD^2=BD^2+CD^2...\Rightarrow a^2=\left(AB+AD\right)^2+\left(AC-AD\right)^2\)
\(\Rightarrow AB^2+2AB.BD+AD^2+AC^2-AD^2\Rightarrow a^2=b^2+c^2+2c.AD=b^2+c^2+bc\left(AD=\frac{1}{2}b\right)\)

D A C B b c a b/2
Ta có: \(\widehat{CAB}=120^o\Rightarrow\widehat{CAD}=60^o\)
\(\Rightarrow\Delta DAC\) là nửa tam giác đều.
\(\Rightarrow AD=\frac{AC}{2}=\frac{b}{2}\)
Xét \(\Delta CDB\) vuông tại D có:
\(CB^2=CD^2+DB^2=\left(AC^2-AD^2\right)+\left(AD+AB\right)^2\)
\(\Leftrightarrow CB^2=AC^2-AD^2+AD^2+2AD.AB+AB^2=AC^2+2AB.\frac{AC}{2}+AB^2\)
\(\Leftrightarrow a^2=b^2+c^2+bc\)

Kẻ đường cao BD ứng với AC. Do góc A tù \(\Rightarrow\) D nằm ngoài đoạn thẳng AC hay \(CD=AD+AC\) và \(\widehat{DAB}=180^0-120^0=60^0\)
Áp dụng định lý Pitago:
\(AB^2=BD^2+AD^2\) \(\Rightarrow BD^2=AB^2-AD^2\)
Trong tam giác vuông ABD:
\(cos\widehat{BAD}=\dfrac{AD}{AB}\Rightarrow\dfrac{AD}{AB}=cos60^0=\dfrac{1}{2}\Rightarrow AD=\dfrac{1}{2}AB\)
\(\Rightarrow BD^2=AB^2-\left(\dfrac{1}{2}AB^2\right)=\dfrac{3}{4}AB^2\)
Pitago tam giác BCD:
\(BC^2=BD^2+CD^2=\dfrac{3}{4}AB^2+\left(AD+AC\right)^2\)
\(=\dfrac{3}{4}AB^2+\left(\dfrac{1}{2}AB+AC\right)^2\)
\(=\dfrac{3}{4}AB^2+\dfrac{1}{4}AB^2+AB.AC+AC^2\)
\(=AB^2+AB.AC+AC^2\)
Hay \(a^2=b^2+c^2+bc\)